1. Геометрия
  2. Дан параллелограмм ABCD.

Дан параллелограмм ABCD. На сторонах BC и CD взяты соответственно точки M и N так, что CM : MB = 2 : 1 и CN : ND = 2 : 1. Найдите площадь треугольника AMN, если площадь параллелограмма ABCD равна 54

Дахич1 Дахич1    3   14.07.2020 10:55    9

Ответы
Galerina Galerina  15.10.2020 15:21

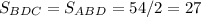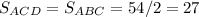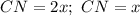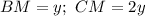Проведём диагонали AC и BD. Диагональ параллелограмма делит на два равных треугольника и их площади равны: S_{BDC}=S_{ABD}=54/2=27 и S_{ACD}=S_{ABC}=54/2=27. Пусть CN=2x;~ CN=x и BM=y;~ CM=2y. Тогда

\dfrac{S_{BDC}}{S_{MCN}}=\dfrac{3y\cdot 3x}{2y\cdot 2x}=\dfrac{9}{4} откуда S_{MCN}=12.

\dfrac{S_{ACD}}{S_{AND}}=\dfrac{3x\cdot 3y}{x\cdot 3y}=3 откуда S_{AND}=9

\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{3x\cdot y}{3x\cdot 3y} откуда S_{ABM}=9

S_{AMN}=S_{ABCD}-S_{MCN}-S_{AND}-S_{ABM}=24— ответ.


Дан параллелограмм ABCD. На сторонах BC и CD взяты соответственно точки M и N так, что CM : MB = 2 :
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
AdelinaAries AdelinaAries  28.09.2019 19:20
Промінь вк ділить кут авс на два кути, причому кут авк удвічі більший за кут квс. знайдіть кут між бісектрисою кута авс і променем вк, якщо кут авс прямий....
Hasky12 Hasky12  28.09.2019 19:20
Разность двух смежных углов равна 16 градусов. найдите меньший из этих углов...
Bessihatanuamailru Bessihatanuamailru  28.09.2019 19:20
Найдите угол, смежный с углом 115 градусов...
kwjeps kwjeps  28.09.2019 19:20
Может ли выпуклый четырёх угольник являться параллелограммом только по противоположным равным углам?...
azizka4 azizka4  28.09.2019 19:20
Дан куб abcda1b1c1d1 точки mn и k- середины ребёр а1в1, аа1 и ad сответсвенно. найдите угол между mn и kn...
micser2017 micser2017  28.09.2019 19:20
Abcd-параллелограмм; ак- биссектриса угла а; угол каd=40°; (•)к принадлежит вс; ав= 8см., кс= 2см. найти: углы а,в,с,d; bc, cd, ad с решением!...
ggvpizi09 ggvpizi09  09.12.2021 12:28
Знайти довжину кола з радіусом 12 см...
vladavlada60 vladavlada60  09.12.2021 12:27
Сколько бисектрис имеет триугольник...
kiss123kiss kiss123kiss  09.12.2021 12:26
Укажіть значення n, при якому вектори a (n;3) і b (-2;-4) є перпендикулярними...
polina359674 polina359674  09.12.2021 12:25
Дано векторы а(0:-4), b(-6:0), c (-12:8) a) найти вектор m=2a-3b+c и его длина б)найти угл между вектора и a и b...

Популярные вопросы