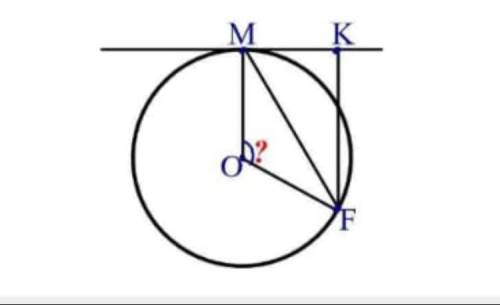
Через точку F ,лежащую на окружности, восстановлен перпендикуляр FK к касательной к окружности(M-точка касания). MK=5, MF=10. Найдите центральный угол MOF. ответ дайте в градусах. С РЕШЕНИЕМ !!

Добрый день! Давайте решим вашу задачу. Мы знаем, что перпендикуляр FK проведен через точку F касательной к окружности в точке M, а также известны значения MK = 5 и MF = 10. По определению окружности, касательная, проведенная из точки M, будет перпендикулярна радиусу, проведенному в эту точку. То есть, MO будет перпендикулярно MK. Так как MK = 5, то MO также будет равен 5. Мы знаем, что MF - это радиус окружности, и он равен 10. Теперь мы можем построить треугольник MFO, где MO = 5 и MF = 10. Для нахождения центрального угла MOF, нам необходимо использовать теорему косинусов. Эта теорема позволяет нам найти угол треугольника, если известны длины всех его сторон. Теорема косинусов гласит: c^2 = a^2 + b^2 - 2ab * cos(C), где a, b, c - длины сторон треугольника, а C - угол, противолежащий стороне длиной с. В нашем треугольнике MOF, сторона MO = a, сторона OF = b, а сторона MF = c. Таким образом, мы можем записать: MF^2 = MO^2 + OF^2 - 2 * MO * OF * cos(MOF). Подставим значения: 10^2 = 5^2 + OF^2 - 2 * 5 * OF * cos(MOF). 100 = 25 + OF^2 - 10OF * cos(MOF). Перенесем все в одну сторону: OF^2 - 10OF * cos(MOF) + 75 = 0. Теперь нам нужно решить это квадратное уравнение относительно OF. Для этого воспользуемся дискриминантом: D = b^2 - 4ac, где a = 1, b = -10, c = 75. D = (-10)^2 - 4 * 1 * 75 = 100 - 300 = -200. Дискриминант D отрицательный, что означает, что уравнение не имеет решений в действительных числах. Однако, поскольку речь идет о геометрической задаче, мы должны помнить, что OF - это длина отрезка, и никакие другие значения OF, кроме положительных, не могут быть приняты. Таким образом, OF не может быть равен 0, и мы должны сделать предположение, что OF - это положительное действительное число. Теперь мы можем использовать теорему косинусов для решения уравнения: OF = (10 * cos(MOF) + √(-200)) / 2. Мы видим, что внутри корня находится отрицательное число, что означает, что у нас нет действительного решения. Таким образом, у нас нет решения для MOF в действительных числах. В заключение, ответ на ваш вопрос - центральный угол MOF не имеет действительного значения в градусах.