Биссектриса ВН равнобедренного треугольника АБС образует с его боковой стороной угол,равный 60°.Отрезок МН- высота треугольника НБС.Найдите отрезок ВМ,если боковая сторона ВС треугольника АБС равна 12см ХЕЛП МИ
Другие вопросы по теме Геометрия
Популярные вопросы
- Теоретичний матеріал про міміку...
1 - True/False 1. Robots are mechanical and virtual machines. 2. The term robot...
1 - Вариант 4 1. Выполните действия: 1) 3,7 + (–8,5); 4) –4,8 + 4,8; 7) –2,8...
1 - Questions: 1. Pourquoi la situation écologique s aggrave?2. Qu est-ce que...
2 - 7:00 утра пассажирский самолёт вылетел из города А после полчаса остановки...
1 - під час пропускання сульфур (IV) оксиду крізь розчин барій гідроксиду утворилась...
1 - очищенные от косточек сливы при сушке теряют 7/8 своей массы,что составило...
3 - с английским ( Present Simple / Present Continuous) 1. Children ( make )...
1 - 2. Сізге «Қазақстанның қазба байлықтары» тақырыбында реферат жазуға тапсырылды....
2 - Практическая работа «Влияние природных условий и ресурсов на отрасли специализации...
2
В прямоугольном треугольнике НВС, угол Н - прямой, угол В = 60, ВС = 12см. В этом же треугольнике:
sinB = НС/ВС
1/2 *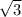 = НС/12
= НС/12
НС = 6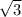 см
см
угол С = 30
cosC = МС/НС
1/2 *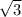 = МС/6
= МС/6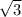
МС = 9 см
ВМ = 12-9 = 3см
ответ: 3см
ответ:BM = 3cm
Объяснение: угол АВС=120°,уголы ВАС=ВСА=30°,ВН в равнобедренном треугольнике является высотой,медийной и биссектрисой.Треугольник ВНС прямоугольный,угол ВСА=30°следовательно ВН=ВС÷2,ВН=12÷2=6см;треугольник ВНМ прямоугольный угол НВС=60°(по условию),тогда угол ВНМ=30°. ВН- гипотенуза,ВМ=ВН÷2=6÷2=3см,т.к. ВМ лежит против 30°. ответ: 3см