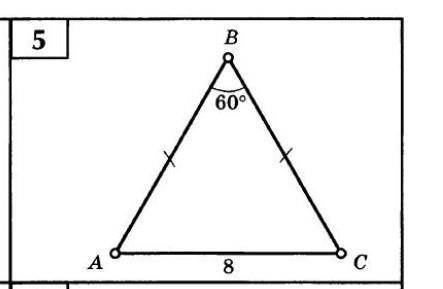
AC=8
угол B=60°
Нужно найти площадь треугольника.​

решение на фотографии

Для решения этой задачи, мы можем использовать формулу для вычисления площади треугольника на основе длин его сторон и углов.

Формула площади треугольника:
Площадь = (1/2) * a * b * sin(C)

Где:
- "a" и "b" - это длины двух сторон треугольника,
- "C" - это угол между этими двумя сторонами.

В задаче у нас дано:
AC = 8 - это длина стороны треугольника
Угол B = 60° - это угол между сторонами AC и BC

1. В первую очередь, нам нужно найти длину стороны BC треугольника. Для этого можем использовать теорему косинусов.

Теорема косинусов:
c^2 = a^2 + b^2 - 2*a*b*cos(C)

Где:
- "c" - длина третьей стороны треугольника (BC),
- "a" и "b" - длины двух других сторон треугольника (AC и AB),
- "C" - угол между сторонами "a" и "b".

Подставим известные значения:
AC = 8, угол B = 60°, а BC - длина стороны треугольника, которую мы и хотим найти.

c^2 = 8^2 + b^2 - 2*8*b*cos(60°)

2. Теперь, мы можем решить уравнение, чтобы найти значение BC:

64 + b^2 - 16b = 0

b^2 - 16b + 64 = 0

Данное квадратное уравнение можно решить двумя способами: через факторизацию квадратного трехчлена или с помощью квадратного корня.

Однако, в данном случае мы можем заметить, что полином в квадрате имеет вид (b - 8)^2, поэтому факторизация возможна только таким образом:

(b - 8)^2 = 0

Отсюда получаем, что b - 8 = 0, то есть b = 8.

3. Теперь, когда у нас есть значения длин сторон AC = 8 и BC = 8, а также известное значение угла B = 60°, мы можем использовать формулу для вычисления площади треугольника:

Площадь = (1/2) * a * b * sin(C)

Подставим известные значения:
a = AC = 8
b = BC = 8
C = угол B = 60°

Площадь = (1/2) * 8 * 8 * sin(60°) = 32 * √3 / 2 = 16√3

Площадь треугольника равна 16√3.