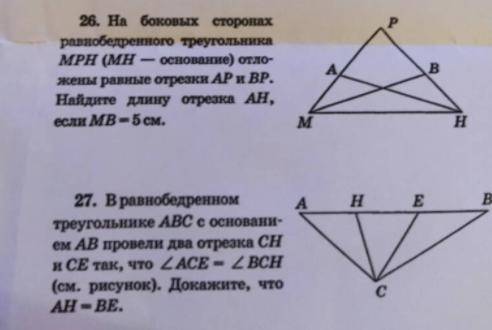
26.На боковых сторонах равнобедренного треугольника MPH (MH - основание) отложены равные отрезки АР и ВР. Найдите длину отрезка АН, еслиМВ=5см. 27.в равнобедреном треугольнике АВС с основанием АВ провели два отрезка СН и СЕ так, что LACE - LBCH (см. рисунок). Докажите, что AH-BE.

Добрый день!

Для решения обоих задач мы будем использовать свойства равнобедренного треугольника. Перейдем непосредственно к решению каждой из задач.

Задача 26.

Для начала обратимся к свойству равнобедренного треугольника, которое гласит: биссектриса угла, образованного боковыми сторонами треугольника и основанием, делит основание на два отрезка, пропорциональных боковым сторонам.

В данной задаче треугольник MPH является равнобедренным с основанием MH.

По условию дано, что отрезки АР и ВР равны друг другу. Обозначим их длину за х.

Так как отрезок АР равен отрезку ВР, то мы можем записать равенство:

АР = ВР = х.

Согласно свойству равнобедренного треугольника, отрезок АН будет равен отрезку НР.

Поэтому, чтобы найти длину отрезка АН, нам необходимо найти длину отрезка НР.

Заметим, что треугольник MPR образует прямоугольный треугольник MNR, где МН - высота треугольника MPR, а МР и НР - катеты.

Тогда по теореме Пифагора для прямоугольного треугольника МНР мы можем записать:

МН² = МР² + НР².

Заметим, что отрезок МР равен половине основания MH (МР = МН / 2), так как основание равнобедренного треугольника делится биссектрисой на два равных отрезка.

Теперь мы можем записать равенство:

(МН / 2)² + НР² = МН².

Раскроем скобки и упростим данное уравнение:

МН² / 4 + НР² = МН².

Перенесем все слагаемые, содержащие МН², на одну сторону уравнения:

НР² = 3МН² / 4.

Теперь найдем значение отрезка МН.

Заметим, что треугольник MPH является равнобедренным, поэтому угол PHM равен углу HPM.

Тогда угол MPH равен 180 - 2 * угол PHM.

Так как треугольник MPH является равнобедренным, угол MPH также равен углу MHP.

Значит, угол MHN будет равен половине угла MPH, то есть (180 - 2 * угол PHM) / 2 = 90 - угол PHM.

Так как треугольник MHN является прямоугольным, а угол HNM равен 90 - угол PHM, то углы М и Н являются смежными углами, а значит, их сумма равна 180 градусам.

Таким образом, углы MHN и HNM являются дополнительными друг другу.

Тогда (90 - угол PHM) + угол PHM = 180.

90 + угол PHM = 180.

угол PHM = 180 - 90 = 90.

Значит, угол MHN также равен 90 градусам.

Теперь, зная угол MHN и длину МН (равную 5 см, так как МВ = 5 см), мы можем использовать функции тригонометрии для нахождения длины НР.

По определению функции синуса, sin(угол) = противолежащий катет / гипотенуза.

В данном случае угол MHN является прямым, поэтому синус этого угла будет равен отношению противолежащего катета НР к гипотенузе МН.

Тогда sin(MHN) = НР / МН.

Подставляем известные значения и решаем уравнение:

sin(90) = НР / 5.

Так как синус 90 градусов равен 1, то уравнение принимает вид:

1 = НР / 5.

Перемножаем обе части уравнения на 5 и решаем полученное уравнение:

5 = НР.

Таким образом, мы получили, что длина отрезка HN равна 5 см.

Так как отрезок АН равен отрезку НР, то мы можем заключить, что длина отрезка АН также равна 5 см.

Ответ: длина отрезка АН равна 5 см.

Задача 27.

Дано: равнобедренный треугольник АВС с основанием АВ, отрезки СН и СЕ. Требуется доказать, что АН - ВЕ.

Обозначим угол М после поворота отрезка АЕ за угол АМЕ.

Так как треугольник АВС равнобедренный, углы А и В будут равными.

Доказательство:

1. Из условия задачи известно, что угол LACE равен углу LBCH.

Поэтому, угол LAC будет равен углу LBH.

2. Отрезок СЕ параллельно отрезку АВ, так как они расположены на одной вертикальной прямой.

Тогда мы можем использовать одну из теорем о сумме углов при пересечении прямых. В данном случае это теорема об альтернативных углах.

Согласно данной теореме, угол LAC будет равен углу В, так как они являются альтернативными углами.

Из пункта 1 мы знаем, что угол LAC равен углу LBH.

Таким образом, угол LBH равен углу В.

3. Для дальнейшего рассуждения нам понадобится свойство равнобедренного треугольника, которое утверждает: если из верхнего основания провести линию между вершинами боковых сторон, то она будет являться биссектрисой в равнобедренном треугольнике и делить противолежащий угол на два равных угла.

В данном случае, отрезок СН является биссектрисой угла АСВ.

Заметим, что угол CHB является противолежащим углом к боковой стороне СВ.

По свойству биссектрисы, он должен быть равным углу CBH.

4. Так как углы LBH и CBH равны, а BC - общая сторона углов BCH и CBH, то треугольник BCH равнобедренный.

Тогда BH будет равен CH, так как основания равнобедренного треугольника равны.

5. Обратимся к треугольнику АМЕ.

Заметим, что угол АМЕ является равным углу А.

Также мы уже доказали, что угол А является равным углом LBH.

Тогда угол АМЕ равен углу LBH.

6. Так как угол В, равен углу LBH, и угол АМЕ также равен углу LBH, то угол В равен углу АМЕ.

7. Мы доказали, что угол В равен углу АМЕ, а это значит, что у треугольников АНС и ВЕН углы при А и В равны.

Теперь мы можем воспользоваться свойством равнобедренного треугольника, которое утверждает: если у двух треугольников одинаковых углов расположены при одинаковых сторонах, то эти треугольники равны.

Таким образом, треугольники АНС и ВЕН равны, так как у них углы при А и В равны, а стороны НС и ВЕ равны.

Следовательно, их стороны АН и ВЕ также равны.

Доказано: АН равен ВЕ.

Ответ: АН - ВЕ.