10. Найдите площадь прямоугольного треугольника, если один из катетов равен 12 см, а гипотенуза равна 13 см. 1.Найдите площадь ромба, если его диагонали равны 14 и 6.
2.Периметр ромба равен 96, а один из углов равен 30. Найдите площадь ромба.

10) S=30 (см^2)

1) 42

2) 288

Объяснение:

10) Пусть другой катет - x. Найдем другой катет по теореме Пифагора:

Формула: площадь прямоугольника равна половине произведения катетов, т.е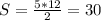 (см^2)

1) По формуле: площадь ромба равна половине произведения диагоналей: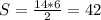

2) P ромба = 4 * сторона ромба, значит сторона ромба равна 96/4=24

По формуле: площадь ромба равна квадрату стороны, умноженному на синус угла, т.е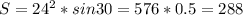

Объяснение:

10)

Дано:

Прямоугольный треугольник

с=13см гипотенуза

а=12см катет

S=?

Решение

По теореме Пифагора найдем второй катет.

b=√(c²-a²)=√(13²-12²)=√(169-144)=√25=5см

S=1/2*a*b=1/2*5*12=30cм²

ответ: 30см²

1)

Дано:

Ромб

d1=6см диагональ

d2=14см диагональ

S=?

Решение

S=1/2*d1*d2=1/2*14*6=42см²

ответ: 42см²

2)

Дано:

Ромб

Р=96ед

<a=3°

S=?

Решение

Р=4а, где а-сторона ромба

а=Р/4=96/4=24ед сторона ромба

S=a²*sin<a=24²*1/2=288ед²

ответ: 288ед²