1) найдите косинусы углов треугольника abc, если a (1; 7) b(-2; 4) c(2; 0) 2)решите треугольник mnk, если угол n=30, k=105 nk=3 корня из 2 с решением

Ответы

Варенье11333333 30.06.2020 16:50

1) Дано : ΔABC; A (1;7); B(-2;4); C(2;0)

Найти : cos A, cos B, cos C

$AB=\sqrt{\big(x_B-x_A\big)^2+\big(y_B-y_A\big)^2}=\\\\~~~~~=\sqrt{\big(-2-1\big)^2+\big(4-7\big)^2}=\sqrt{18}=3\sqrt2\\\\AC=\sqrt{\big(x_C-x_A\big)^2+\big(y_C-y_A\big)^2}=\\\\~~~~~=\sqrt{\big(2-1\big)^2+\big(0-7\big)^2}=\sqrt{50}=5\sqrt2\\\\CB=\sqrt{\big(x_B-x_C\big)^2+\big(y_B-y_C\big)^2}=\\\\~~~~~=\sqrt{\big(-2-2\big)^2+\big(4-0\big)^2}=\sqrt{32}=4\sqrt2$

По теореме косинусов

a² = c² + b² - 2cb·cos α

$\cos\alpha =\dfrac{c^2+b^2-a^2}{2cb}\\\\\\\cos A =\dfrac{AB^2+AC^2-CB^2}{2\cdot AB\cdot AC}=\dfrac{\sqrt{18}^2+\sqrt{50}^2-\sqrt{32}^2}{2\cdot 3\sqrt2\cdot 5\sqrt2}=\\\\~~~~~~~=\dfrac{18+50-32}{2\cdot 3\cdot 5\cdot2}=\dfrac{36}{60}=\dfrac 35\\\\\\\cos B =\dfrac{AB^2+CB^2-AC^2}{2\cdot AB\cdot CB}=\dfrac{\sqrt{18}^2+\sqrt{32}^2-\sqrt{50}^2}{2\cdot 3\sqrt2\cdot 4\sqrt2}=\\\\~~~~~~~=\dfrac{18+32-50}{2\cdot 3\cdot 4\cdot2}=\dfrac{0}{48}=0$

$\cos C =\dfrac{AC^2+CB^2-AB^2}{2\cdot AC\cdot CB}=\dfrac{\sqrt{50}^2+\sqrt{32}^2-\sqrt{18}^2}{2\cdot 5\sqrt2\cdot 4\sqrt2}=\\\\~~~~~~~=\dfrac{50+32-18}{2\cdot 5\cdot 4\cdot2}=\dfrac{64}{80}=\dfrac45$

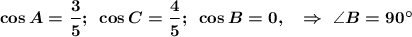
ответ : $\boldsymbol{\cos A=\dfrac 35;~\cos C =\dfrac 45;~\cos B=0,~~\Rightarrow~\angle B=90\textdegree}$

============================================

Дано : ΔMNK; ∠N=30°; ∠K=105°; NK=3√2

Найти : ∠M, MN, MK,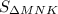 $S_{\Delta MNK}$

Решение : сумма углов треугольника равна 180° ⇒

∠M = 180° - (∠N + ∠K) = 180° - (30° + 105°) = 45°

По теореме синусов

$\dfrac{NK}{\sin M}=\dfrac{MK}{\sin N}~~~\Rightarrow~~MK=\dfrac{NK\cdot \sin N}{\sin M}\\\\MK=\dfrac{3\sqrt2\cdot \sin 30\textdegree}{\sin 45\textdegree}=\dfrac{3\sqrt2\cdot \frac 12}{\frac{\sqrt2}2}=3\sqrt2\cdot \dfrac 12\cdot \dfrac2{\sqrt2}=3$

Проведём высоту KH⊥MN

ΔKHN - прямоугольный

$NH = NK\cdot \cos 30\textdegree=3\sqrt2\cdot \dfrac{\sqrt3}2=1,5\sqrt6$

ΔKHM - прямоугольный

$MH = MK\cdot \cos 45\textdegree=3\cdot \dfrac{\sqrt2}2=1,5\sqrt2$

$MN = MH + NH = 1,5\sqrt2+1,5\sqrt6=1,5\sqrt2\big(1+\sqrt3\big)$

$S_{\Delta MNK}=\dfrac 12\cdot MN\cdot NK\cdot \sin 30\textdegree=\\\\~~~~~=\dfrac 12\cdot 1,5\sqrt2\big(1+\sqrt3\big)\cdot 3\sqrt2\cdot \dfrac 12=2,25\big(1+\sqrt3\big)$