1)Используя данные на чертеже решите задачу(найти х

Объяснение:

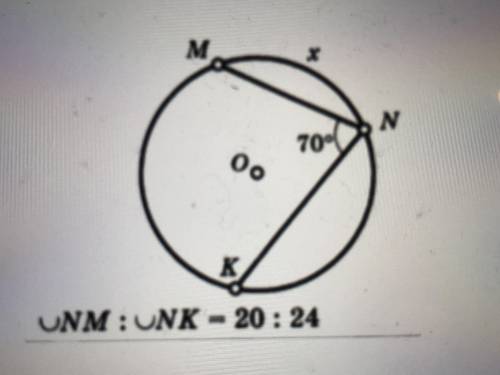
1) ∪ МК=70°*2=140° (∠KNM-вписанный)

⇒ ∪ MNK=360°-140°=220°

Пусть ∪ NM=20y⇒ ∪ NK=24y

20y+24y=220

44y=220

y=5°

⇒ ∪ NM=20y=100°

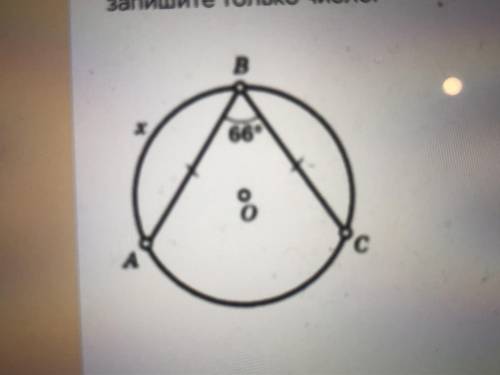
2) ∪ АС=66°*2=132° (∠АВС-вписанный)

∪ АВС=360°-132°=228°

∪ АВ=∪ВС=228°:2=114° (равные хорды отсекают равные дуги)

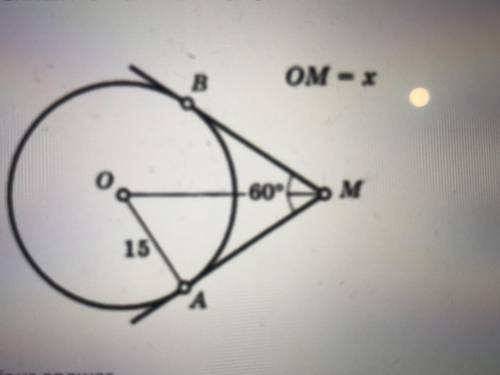
3)ОМ-биссектриса ∠М (св-во вписанной окружности)

⇒∠АМО=30°

ΔАОМ-прямоугольный (радиус ⊥касательной)

АО=2ОА=30 (кактет, лежащий против ∠30°)

2) x = 144

2)

AC = AOC = ABC × 2 (как центральный)

AOC = AC = 66 × 2 = 132

Т.к. Сторона AB = стороне BC, следует:

x = AB = (360 - 132) : 2 = 144

x = 144