Знайдіть знаменник геометричної прогресії і суму семи перших її членів, якщо перший і третій члени відповідно дорівнюють 27
і 3, а всі члени її додатні.
Другие вопросы по теме Алгебра
Популярные вопросы
- Объём водорода при (н.у)который потребуется для синтеза 80 л сероводорода...
3 - Укажи, где будет каждый лыжник за 1 час движения, если они вышли одновременно...
1 - Причини та наслідки Паризької комуни...
1 - agar kuchaytirish koiffisenti 500ga, tordagi kuchlanish ozgarishi 50 ga...
1 - Нужна ! Задние: выделить грамматическую основу в следующих предложениях:...
2 - От пункта А до Б электричка проходит за 2 часа 30 минут, а поезд на 40...
1 - Выполните умножение. а) 3x (2x2 – 5); в) 5y( 3/4х - 4 ); б) a2 (a + 2);...
1 - идеальный газ, который перешел из состояния 1 в состояние 2, показанное...
2 - 6. В два сосуда налито разное количество воды (рис. 126). В каком сосуде...
2 - Нужно подчеркнуть герундий, написать какую функцию он выполняет (к примеру...
2
знаменник геометричної прогресії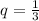
суму семи перших членів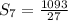
Объяснение: