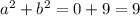Задание : если для рациональных чисел а и b выполняется равенство
, то найдите значение выражения
Варианты ответа: 7 ;9 ; 13 ;27
Заранее благодарю!
(в моих вопросах также есть другие нерешенные задания, буду благодарна, если заглянете))
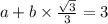
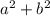
Другие вопросы по теме Алгебра
Популярные вопросы
- Информатика 3 класс фгос-рабочая тетрадь 1 часть. к параграфу 5,...
1 - Воказании ветеранам войны и труда принимали участие 96 пионеров....
2 - Как перевести число 1999 в двоичную систему счисления?...
1 - Побудувати діалог зі словами бавовна, верстат, вовна, волокно,...
3 - Старуха шапокляк решила приручить носорога. каждый день она скармливала...
3 - Hello! my name is polly scott. i m from leeds. i have a son and...
3 - Вмарте 1946г. верховным советом был принят закон о четвертом пятилетнем...
3 - Вычислите массовую долю в процентах ортофосфорной кислоты в растворе...
2 - Определить связи между неживой и живой природой; растениями и животными;...
1 - Решите найдите координаты точки пересечения графиков функций y=...
3
9
Объяснение:
Система уравнений
Всегда имеет два решения, начиная с некоторого значения параметра с.
В задании говорится, что a и b рациональные числа.
Выразим из первого уравнения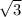
Как известно,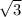 число иррациональное и не может быть выражено через рациональные числа. Поэтому запишем последнее равенство в виде
число иррациональное и не может быть выражено через рациональные числа. Поэтому запишем последнее равенство в виде 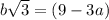 Равенство имеет место только когда левая и правая часть равны 0. Отсюда
Равенство имеет место только когда левая и правая часть равны 0. Отсюда 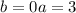 . Тогда
. Тогда