Y(x)=x^3-4x^2+3 завтра зачет полное исследование функции взамен если нужна говорите

Ответы

Alina18181 28.05.2020 03:27

Исследование функции

1) область определения
$\displaystyle y=x^3-4x^2+3$
Функция определена и непрерывна на всей числовой прямой
D(y)=R
(Это очень хорошо, отпадают вертикальные асимптоты)

2) Проверим функцию на чётность/нечётность
$\displaystyle y(-x)=(-x)^3-4(-x)^2+3=-x^3-4x+3\\\\y(-x) \neq y(x); y(-x) \neq -y(x)$

значит, данная функция не является чётной или нечётной.

Очевидно, что функция непериодическая.(т.к. она не является тригонометрической)

3) Асимптоты, поведение функции на бесконечности.

Так как функция непрерывна на R , то вертикальные асимптоты отсутствуют.
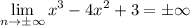
$\displaystyle \lim_{n \to \pm \infty} x^3-4x^2+3= \pm \infty$

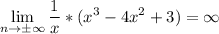
Так как пределы бесконечны, горизонтальных асимптот нет

Найдем вертикальные асимптоты

$\displaystyle \lim_{n \to \pm \infty} \frac{1}{x} *(x^3-4x^2+3) = \infty$

Значит наклонных асимптот тоже нет

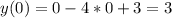
4) Определим точки пересечения графика функции с осями координат
х=0
$\displaystyle y(0)= 0-4*0+3=3$

Пересечение с осью ОУ в точке (0;3)

у=0

$\displaystyle x^3-4x^2+3=0\\\\ (x-1)(x^2-3)=0\\\\x_1=1; x_2= \sqrt{3}; x_3=- \sqrt{3} 

$

Пересечение с осью ОХ (1;0) ; (√3;0) ; (-√3;0)

5) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции
$\displaystyle y`=(x^3-4x^2+3)`=3x^2-8x\\\\y`=0\\\\ x(3x-8)=0\\\\x_1=0; x_2=8/3$

Точки х=0 и х=8/3 точки экстремума функции

__+_____0______-____8/3___+__

возр убыв возр

Значит х= 0 точка максимума у(0)=3
Значит точка х=8/3 точка минимума у(8/3)= -175/27

на промежутке (-оо; 0) возрастает
на промежутке (0; 8/3) убывает
на промежутке (8/3; +oo) возрастает

6) Исследуем функцию на перегибы и выпуклость
$\displaystyle y``=(3x^2-8x)`=6x-8\\\\y``=0\\\\6x-8=0\\\\x=8/6=4/3
$

значит х=4/3 точка перегиба

_-_____ 4/3__+____

выпуклая/ вогнутая

7) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
х=2 y(1)=2³-4*2²+3=8-16+3= -5

х= -2 y(-2)= (-2)³-4*(-2)²+3=-8-16+3=-21

теперь по полученным данным построим график