Y'+2y+4=0. y(0)=5
решить
Другие вопросы по теме Алгебра
Популярные вопросы
- Наиболее урбанизированная страна Восточной Европы...
2 - Наибольшая испаряемость характерна для природной зоны...
1 - Наиболее сейсмически активные районы России...
2 - Наиболее ярким примером взаимодействия океана с материками служат ветры...
3 - Наибольшая высота Солнца над горизонтом в полдень...
2 - Наиболее освоенные горные территории и весомое число горных жителей в регионе...
1 - Наибольшая среднегодовая величина абсолютной влажности наблюдалась...
1 - Наиболее тонкая земная кора под...
2 - Наибольшее количество осадков в горах Жонгарского Алатау приходится на...
2 - Наибольшее значение для жизни на Земле имеет...
1
Рассмотрим начальное условие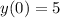 :
:
Получим частное решение: