Втреугольнике авс отмечены середины м и n сторон вс и ас соответственно. площадь треугольника сnm равна 57. найдите площадь четырехугольника авм n

MN - средняя линия, MN || AB. Так как у треугольников MNC и ABC общий угол С и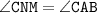 как соответственные углы, то треугольники MNC и ABC подобны.

Средняя линия треугольника равна половине длины параллельной стороны.

MN = AB/2 , значит коэффициент подобия k=1/2.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть

кв. ед.

Площадь четырехугольника ABMN равна:

кв. ед.

ответ: 171 кв. ед.