В сектор 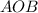 радиуса
радиуса 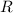 с центральным углом 2α вписали прямоугольник наибольшей площади, симметричный оси симметрии сектора. Найдите площадь такого прямоугольника.
с центральным углом 2α вписали прямоугольник наибольшей площади, симметричный оси симметрии сектора. Найдите площадь такого прямоугольника.
Другие вопросы по теме Алгебра
Популярные вопросы
- 2. Из центра окружности О к хорде АВ, равной 20 см, проведен перпендикуляр...
1 - Ерлан Жүністің «Менің атым – Тәуелсіздік» өлеңінің идеясын түсіндіріп,...
1 - 9. К органам дыхательной системы птиц от- 1. носятся:а) клюв;г) легочные...
1 - Как решить неравенство:⁵/7...
2 - Характерні ознаки жанру РОНДО,Його будова?...
2 - 16) Порівняйте між собою гриби й рослини. Укажіть риси схо-жості й відмінності....
2 - быстрее у меня сор Определи аналитический зависимости заданной табличным...
3 - 4- тапсырма: Өлеңдер бойынша Венн диаграммасын толтыр. 2 айырмашылық,...
2 - Знайдіть суму всіх кутів 19-тикутника...
1 - 11x- 5y = 8 2x + 4y = 26 варианты ответа ( 2; 8) ( 4; 8) ( 8; 2) ( 2;...
3
2R²
Объяснение:
если надо найти прямоугольник наибольшей площади надо взять отрезок от R/2 и спустить в окружность, если угол сектора четный то получим что тот расстояние от R/2 до окружности равна R;
а длина от R/2 до другой R/2 получиться 2R;
S=R•2R=2R²;