Упростите выражение до числового значения
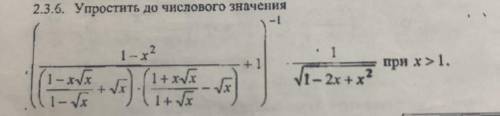
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой праздник для православных самое главное объясни почему ☺ кому...
1 - Два велосипедиста выехали из лагеря в противоположных направлениях....
2 - Мэри поппинс пролетела под зонтом на юг 12 км 451 м. затем ветер поменял...
3 - Найдите значение разности а-(b-c), если: а=минус35,b=14, c =21, 2)a=минус16,...
3 - Решите ! (20 16/25 + 13 9/ 4/14 +7 13/14) по действие...
3 - Определите соотношение массы соли и массы воды для образования раствора...
1 - Составить на тему найти площадь круга...
3 - Охарактеризуйте политику ивана грозного направленную на установление...
2 - При подготовке к олимпиаде миша решал . в первую неделю он решил 55%...
1 - Сколько граммов содержат 3/10 я не поняла тему на этом примере объясните...
2
ответ: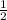
Объяснение:
Продолжение: