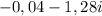Срешением комплексного числа.
(1-i)^5-1 / (1+i)^5+1
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислить используя рисунок sin 135...
2 - Какой цифрой оканчивается результат вычисления 3 в степени 2016...
2 - Дан фрагмент программы на алгоритмическом языке: i=1 a[1]: =1...
2 - Написать программу вычислить значение выражения (1+2)(1+2+3)...
3 - Сусловием.мартышка сорвала две грозди бананов.в одной. 10 бананов,в...
3 - Условия при которых все варианты генотипа гибридных особей проявляются...
2 - Выполните умножение. а) 2 1/3 * 2; б) 4 * 1 1/2; в) 1 1/3 *...
3 - Из цифр 1 и 5 сочтавляют десятичное число кратное 9 сколько...
3 - Чем отличается повседневняя рубаха от праздничной?...
2 - Написать present simple tens твой друг сейчас готовит обед....
3
Воспользуемся формулой биноминального разложения двучлена
для 5-ой степени: (a+b)⁵ = a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
1)
2)
3)
ответ: