1. Алгебра
  2. с решением этих трёх заданий

с решением этих трёх заданий нужно И если можно, то с полными вариантами решений.


с решением этих трёх заданий нужно И если можно, то с полными вариантами решений.

ArtyomKashin ArtyomKashin    3   16.08.2020 18:42    0

Ответы
23v 23v  15.10.2020 15:58

19.

Замена переменной:

\sqrt{x^2-y^2}=u     ⇒      x^2-y^2=u^2

\sqrt{x-y}=v         ⇒     x-y=v^2

\left \{ {{u+v=6} \atop {u^2-v^2=12}} \right.            \left \{ {{u+v=6} \atop {(u-v)(u+v)=12}} \right.       \left \{ {{u+v=6} \atop {(u-v)\cdot 6=12}} \right.       \left \{ {{u+v=6} \atop {u-v=2}} \right. сложения:   \left \{ {{2u=8} \atop {v=6-u}} \right.

u=4; v=2

\left \{ {{\sqrt{x^2-y^2}=4 } \atop {\sqrt{x-y}=2 }} \right.      \left \{ {{x^2-y^2=16} \atop {x-y=4}} \right.       \left \{ {{(x-y)(x+y)=16} \atop {x-y=4}} \right.        \left \{ {{4\cdot (x+y)=16} \atop {x-y=4}} \right.      \left \{ {{x+y=4} \atop {x-y=4}} \right.

сложения:  2х=8;  x=4; y=0

О т в е т. (4;0)

20.

(36^{sinx})^{cosx}=(6^2)^{sinx\cdot cosx}=6^{2sinx\cdot cosx}

6^{2sinx\cdot cosx}=6^{\sqrt{3} cosx}     ⇒   2sinx\cdot cosx=\sqrt{3} cosx

2sinx\cdot cosx-\sqrt{3} cosx=0

cosx\cdot(2sinx-\sqrt{3})=0

cosx=0                      или                2sinx-\sqrt{3}=0   ⇒   sinx=\frac{\sqrt{3} }{2}

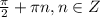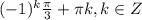
x=\frac{\pi }{2}+\pi n, n \in Z       или              x=(-1)^{k}\frac{\pi }{3} +\pi k, k \in Z

О т в е т.        \frac{\pi }{2}+\pi n, n \in Z  ;  (-1)^{k}\frac{\pi }{3} +\pi k, k \in Z

Отрезку [2π; 3π]  принадлежат корни: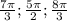\frac{7 \pi}{3} ; \frac{5 \pi}{2} ;\frac{8 \pi}{3}

21.

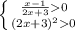
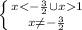
ОДЗ:        \left \{ {{\frac{x-1}{2x+3}0 } \atop {(2x+3)^20}} \right.    \left \{ {{x < -\frac{3}{2}\cup x 1 } \atop {x\neq-\frac{3}{2} }} \right.

x∈(-∞;  -1,5) U(1;+∞)

2log_{2}\frac{x-1}{2x+3} +log_{2}(2x+3)^2\geq 2

По свойству логарифма степени:

log_{2}(\frac{x-1}{2x+3})^2 +log_{2}(2x+3)^2\geq 2

Заменим сумму логарифмов логарифмом произведения:

log_{2}(\frac{x-1}{2x+3})^2 \cdot (2x+3)^2\geq 2

log_{2}({x-1)^2 \geq 2

log_{2}({x-1)^2 \geq log_{2}4

Логарифмическая функция с основанием 2 возрастающая, поэтому

(x-1)^2\geq 4        ⇒     (x-1)^2- 4\geq0

(x-1-2)(x-1+2)\geq 0

(x-3)(x+1)\geq 0

x∈(-∞;-1] U[3;+∞)

Найденные решения входят в ОДЗ,

О т в е т. (-∞;-1] U[3;+∞)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
pety1234 pety1234  29.04.2020 15:54
Б. -0,0.в. о, о, —6. Складіть зведене квадратне рівняння, коренями якого є числа -8 и 3.А. x - 24x-11= 0. Б. -8х + 3x = 0. В. x - 5x - 24 = 0 г. x +5x - 24 = 0.атаn uinniepнь навчальних...
vvozmisheva2 vvozmisheva2  29.04.2020 15:54
Найдите неопределённый интеграл. буду очень признательна!!...
astahovanadezh astahovanadezh  29.04.2020 15:54
Умножьте одно из уравнений системы на такое число,чтобы с сложения можно было исключить одну из переменных 2a-3b=1 4a+2b=3...
yliachedrina200 yliachedrina200  29.04.2020 15:54
Дан ряд чисел 11 12 13 12,5 11 11,5 13 найдите их среднее арифметическое. отметьте данные числа на числовой оси. определите размах ряда. определите стандартное отклонение этого...
yagunovaliza yagunovaliza  29.04.2020 15:54
Розкладіть на множники квадратний тричлен 1)x²-4x-32 2)4x²-15x+9...
angelinashushi angelinashushi  07.06.2021 22:38
Из формулы объема цилиндра V =πr²h выразите r. Сколько корней имеет уравнение 2х2 – 3х + 2 = 0? А. О дин Б. Два В. Ни одного...
sonyasm2006 sonyasm2006  07.06.2021 22:28
Что нужно знать, чтобы ответить по этому графику на вопросы, аналогичные предыдущим?  Сформулируйте (найдите в учебнике) и запишите теорему о достаточных условиях возрастания и...
Doshik131 Doshik131  07.06.2021 22:22
Решите , очень надо, (хотя будет написано 10..) Для функции y=2x³-15x²-36x найди промежутки монотонности, экстремумы, промежутки выпуклости, точки перегиба.​...
Сергей1901 Сергей1901  07.06.2021 22:17
Вроде как просто должно быть, но вот не знаю механизма решения... Для каждого значения a решите неравенство: |x+1| =2a-1...
900901 900901  07.06.2021 22:17
Кусок фольги имеет форму квадрата. Когда от него отрезали полосу шириной 4 см, его площадь стала равна 45см2. Какова длина первоначального куска фольги?...

Популярные вопросы