Вроде как просто должно быть, но вот не знаю механизма решения... Для каждого значения a решите неравенство:
|x+1|<=2a-1
Другие вопросы по теме Алгебра
Популярные вопросы
- Поставить глагол в скобках в нужную форму настоящего совершенного времени...
2 - Какие черты русского национального характера нашли отображение в оюразе Василия...
1 - Какое государство стало образцом для Павла 1?...
3 - Ребят очень надо сдать к 15:00....
1 - Упражения 1,2,4 страница 132 русский язык 4 класс ВЕНТАНА ГРАФ 2 ЧАСТЬ...
3 - Появление побегов на корнях - это размножения: А) корневыми отпрысками; Б)...
3 - В 612году до н. э. столица Ассирийского государства город Ниневия был захвачен...
3 - 10. В магазине было 59 телевизоров. Дообеда продали 20 телевизоров, а послеобеда...
1 - Структурные формулы 2 этилгексадиен - 1,4...
2 - Заполнить таблицу по технологии...
3
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если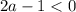 , то есть
, то есть 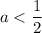 .
.
Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если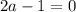 , то есть
, то есть 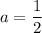 .
.
Получаем неравенство:
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
3. Если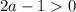 , то есть
, то есть 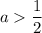 , то получаем неравенство с положительной правой частью:
, то получаем неравенство с положительной правой частью:
Заменим его следующим двойным неравенством:
Таким образом получаем ответ:
при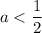 : решений нет
: решений нет
при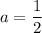 :
: 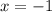
при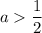 :
: ![x\in[-2a;\ 2a-2]](/tpl/images/2004/6663/9d563.png)