Решите уравнение используя свойства монотонности a)x^5+9x+10=0 б)x^3+2x-33=0

а)

Рассмотрим две функци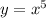и: и 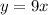. Обе эти функции возрастающие. Тогда и функция, представляющая сумму эти[ функций, то есть функция 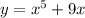будет возрастающей.

Таким образом, в левой части стоит возрастающая функция. Но возрастающая функция принимает каждое свое значение в единственной точке. Это означает, что если найден некоторый корень заданного уравнения, то других корней у уравнения нет.

Корень угадывается достаточно легко: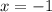 . Проверка:

ответ: -1

б)

Аналогично, каждая из функци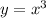й и 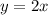возрастает. Значит, возрастает и функция .

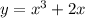Таким образом, уравнение имеет не более одного корня. Этот корень также легко подбирается: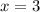 . Проверка:

ответ: 3