Ctg(π/2x−π)=1
решить уравнение
Ответы

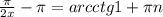 , где n∈Z
, где n∈Z
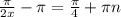
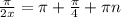
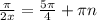
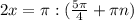
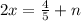 | : 2
| : 2
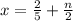
Другие вопросы по теме Алгебра
Популярные вопросы
- 2. В каком году Тамгалы вошел в список Всемирного культурного наследия ЮНЕСКО?А)...
1 - Списать, расставить знаки препинания. Указать, что соединяет каждый союз:...
1 - Два стальных шарика столкнулись на гладкой поверхности. Радиус первого шарика...
3 - Подскажите 1. Form new words to fill the gaps. 1. John would like to be...
3 - Как называется одна из сфер общественного сознания в которых формируются...
1 - Соотнеси понятие и его определение 1)Арабский халифат 2)халиф3)Эмир...
3 - Подати у вигляді дробу: 5y+1-(5y^2-12y)/(y-2)...
1 - 2. Місцевий час якого міста України буде більший: а) Львів; б) Київ; в)...
3 - Там надо подчеркнуть грамматические основы и подписать чем выражено сказуемое...
3 - Номер 234 составить 2 задачи...
2