решить! Линейное Уравнение
12x-5y=7 x-8
11x+3y=14 4y-8y=27
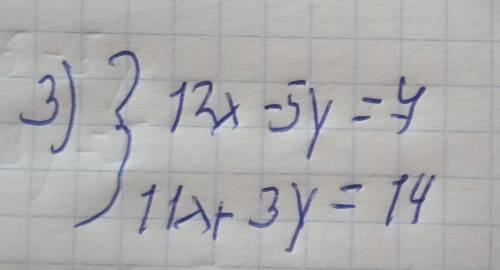
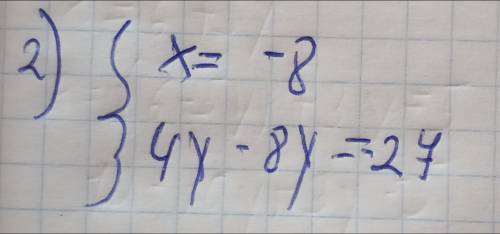
Другие вопросы по теме Алгебра
Популярные вопросы
- Совокупность всех программ, предназначенных для организации диалога с пользователем,...
2 - Як будуть взаємодіяти одна з одною дві скляні палички, наелектрезовані тертям...
2 - есть ли у вас токое сор дайте ! ...
3 - Simple past or present perfectFill in the blanks with the correct form of...
3 - СОР по английскому Read the text and Mark sentences True or False.подпешусь...
3 - С СОРом ПО ЕСТЕСТВО ЗНАНИЮ Что не вместилось в фото:одно нефтегазовое месторождение....
3 - Task 3. Write an article about the celebration in your country or in another...
3 - 3. Розв яжи задачу. Два велосипедисти одночасно від їхали від спільного старту...
3 - Сопротивление медного провода при 0С равно 4 Ом. Найдите его сопротивление...
2 - В схеме представленной на рисунке ε1 = 2,1 В, ε2 = 1,9 В, R1 = 45 Ом, R2 =...
2
1) Начнем с уравнения 12x - 5y = 7x - 8. Нам нужно найти значения переменных x и y. Для этого сначала соберем все x-термы и y-термы на одной стороне уравнения.
12x - 7x = 5y - 8 (перенесем 7x на левую сторону и -8 на правую сторону)
5x = 5y - 8
Теперь проведем то же самое с y-термами:
5x - 5y = -8 (перенесем 5y на левую сторону)
2) Теперь рассмотрим второе уравнение 11x + 3y = 14. Собираем все x-термы и y-термы на одной стороне:
11x - 11x + 3y = 14 - 11x (перенесем 11x на правую сторону)
3y = -11x + 14
3) У нас также есть уравнение 4y - 8y = 27. Собираем все y-термы на одной стороне:
-4y - 8y = 27 (объединяем y-термы)
-12y = 27
Теперь у нас есть система из трех уравнений:
5x - 5y = -8
3y = -11x + 14
-12y = 27
Для решения этой системы уравнений мы можем использовать метод подстановки или метод комбинирования.
Давайте воспользуемся методом подстановки. Из второго уравнения выразим y:
3y = -11x + 14
y = (-11x + 14)/3
Подставим это выражение в первое уравнение:
5x - 5((-11x + 14)/3) = -8
Упростим уравнение:
5x + 55x/3 - 70/3 = -8
(15x + 55x)/3 = -8 + 70/3 (объединим x-термы)
(70x)/3 = -8 + 70/3
Перейдем к следующему шагу:
70x = -8*(3/3) + 70/3 (перемножим каждую дробь на 3)
70x = -24/3 + 70/3
70x = 46/3
Разделим обе стороны на 70:
x = (46/3)/70
x = 46/210
x = 23/105 (получили значение x)
Теперь найдем значение y. Подставим значение x во второе уравнение:
y = (-11*(23/105) + 14)/3
y = (-23/15 + 14)/3
y = (14 - 23*(15/15))/3
y = (14 - 345/15)/3
y = (14 - 23)/15
y = -9/15
y = -3/5 (получили значение y)
Таким образом, решение системы уравнений равно:
x = 23/105
y = -3/5