Пусть a - множество квадратов натуральных чисел, b - множество кубов натуральных чисел. выберите те числа, которые принадлежат пересечению множеств a и b.
вариантов ответа может быть несколько
16
27
64
1
Другие вопросы по теме Алгебра
Популярные вопросы
- Свекла, дедушка, рога, земля, окна. отметить существительные первого...
1 - 1..в каком ряду не со всеми словами пишется слитно? 1)(не)разобранные...
2 - Кого из отгаданных авторов можно выделить из этого ряда? ответ обоснуйте....
2 - Як довго тривали олімпійські ігри у стародавній греції?...
3 - Под ногами3 человеческими3 утоптались3 жёсткие1 кочки и тропа стала канавкой54...
2 - 17 ! среди жителей района 25% составляют дети, а среди взрослого населения...
2 - Розв яжіть рівняння (x^2+x)^2-8(x^2+x)+12=0...
2 - Найти производную функцию y=x^10 ; y=8 корень из х +1/x я не могу решить((...
2 - Мы выиграли так же соревнования по баскетболу...
1 - Сочинение на тему тайга и тундра 8 предложений....
3
Если число n является элементом пересечения А и В, то есть два натуральных числа m и k, для которых выполняется,
Рассмотрим равенство (последовательно преобразовывая его),
Откуда заключаем (т.к. m натурально), что существует такой натуральный d для которого выполнимо,
Подставляя это в равенство, получаем,
Т.е. для того чтобы выполнялось условие,
Должно выполняться условие,
Т.е. только тогда, когда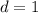 .
.