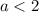При каких значениях параметра a неравенство: 2-x^2(эта запись под корнем)> a+x имеет решения?
Другие вопросы по теме Алгебра
Популярные вопросы
- Вбольшой бидон помещается 15 л молока а в банку - пятая часть молока...
1 - Аты когда-нибудь наблюдала за облаками на что они казались тебе похожими...
3 - Какая кислота имеет следующие характеристики одноосновная кислота держать...
1 - Найдите значение выражения (4 3/2+2 1/5)*16...
1 - Найдите площадь наибольшей грани параллелепипеда с измерениями 3см,...
3 - Представьте в виде степени а(-3 над а) / а ( 7 над а) за ранее большое!...
3 - Где проживает сельское население занятое а) охотой б)земледелием в)...
1 - Прочитай придложэние что их обединяет в первой грппе? а во второй...
2 - При действии бромметана на предельный первичный амин массой 17,7 г...
1 - На 3/7 земельного участка разбит сад ,где 3/4 сада занимает яблони....
3
При каких значениях параметра a неравенство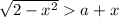 имеет решения?
имеет решения?
ограничения на x: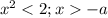
пусть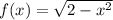 , тогда:
, тогда:
пусть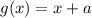 - график прямой, проходящей через (0; a), т.е.
- график прямой, проходящей через (0; a), т.е. 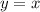 смещённый на a вверх-вниз
смещённый на a вверх-вниз
См. вложения (красным цветом -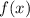 , синим цветом -
, синим цветом - 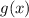 )
)
график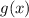 должен находиться ниже графика
должен находиться ниже графика 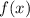
При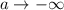 всегда найдётся такой x, что
всегда найдётся такой x, что 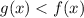
Так будет до касания верхней части окружности (рис.2)
Определим точку касания A:
Её координаты (-1;1), а значит график функции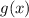 имеет вид
имеет вид 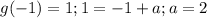
Следовательно при всех a<2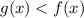 имеет решения
имеет решения
ответ: