Определи такое натуральное значение параметра m , при котором множество решений неравенства (m−x)(10−x)<0 содержит семь натуральных чисел.

Выбери верные варианты ответа:
m=4
m=10
m=17
m=15
m=5
m=3
другой ответ
m=16
m=18
m=2

Семь натуральных чисел из интервала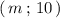    - это числа 9 , 8 , 7 , 6 , 5 , 4 , 3 .

Значит   .

Семь натуральных чисел из интервала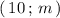    - это числа  11 , 12 , 13 , 14 , 15 , 16 , 17 .

Значит,  

ответ:  m=2  или  m=18 .

Для решения данной задачи, нужно провести анализ неравенства (m-x)(10-x)<0.

Первым шагом, обратим внимание на то, что умножение двух чисел даёт отрицательный результат, когда одно из них положительно, а другое отрицательно.

Разберём возможные варианты для множителей (m-x) и (10-x):

1) Если оба множителя положительны, то и их произведение также будет положительным. Таким образом, (m-x) и (10-x) не могут одновременно быть положительными.

2) Если оба множителя отрицательны, то и их произведение также будет положительным. Таким образом, (m-x) и (10-x) не могут одновременно быть отрицательными.

3) Если один из множителей положителен, а другой отрицателен, то их произведение будет отрицательным. То есть, нам нужно найти такие значения параметра m, при которых один из множителей будет положительным, а другой отрицательным.

Для этого проведём анализ каждого множителя отдельно.

Анализ множителя (m-x):
- Если m-x > 0, то m > x. То есть, m должно быть больше x.
- Если m-x < 0, то m < x. То есть, m должно быть меньше x.
- Если m-x = 0, то m = x.

Анализ множителя (10-x):
- Если 10-x > 0, то 10 > x. То есть, x должно быть меньше 10.
- Если 10-x < 0, то 10 < x. То есть, x должно быть больше 10.
- Если 10-x = 0, то 10 = x.

Теперь, найдём области значений параметра m, для каждого из трёх случаев:

1) Случай m > x и x < 10:
Если m > x и x < 10, то неравенство (m-x)(10-x)<0 будет выполняться только при условии, что оба множителя отрицательны.
То есть, m-x < 0 и 10-x < 0.

m-x < 0
m < x
Таким образом, m должно быть меньше x.

10-x < 0
10 < x
То есть, x должно быть больше 10.

Таким образом, значения параметра m, при которых оба множителя являются отрицательными числами и неравенство выполняется, находятся в интервале (10, ∞).

2) Случай m < x и x > 10:
Если m < x и x > 10, то неравенство (m-x)(10-x)<0 будет выполняться только при условии, что оба множителя положительны.
То есть, m-x > 0 и 10-x > 0.

m-x > 0
m > x
То есть, m должно быть больше x.

10-x > 0
10 > x
Таким образом, x должно быть меньше 10.

Таким образом, значения параметра m, при которых оба множителя являются положительными числами и неравенство выполняется, находятся в интервале (-∞, 10).

3) Случай m = x и x = 10:
Если m = x и x = 10, то неравенство (m-x)(10-x)<0 будет выполняться только при условии, что один из множителей равен нулю, а другой не равен нулю.
То есть, m-x ≠ 0 и 10-x ≠ 0.

m-x ≠ 0
m ≠ x
Значение параметра m должно отличаться от значения переменной x.

10-x ≠ 0
10 ≠ x
Значение переменной x должно отличаться от 10.

Таким образом, значения параметра m, при которых один из множителей не равен нулю, а другой равен нулю и неравенство выполняется, не существует.

Таким образом, из всех предложенных вариантов ответа, единственным корректным является m=10.