Новогодняя задача про тортик. Пусть имеются круглые тортики радиусом R с постоянной высотой.

Маша режет тортик традиционно - разрезами, проходящими через центр тортика на 8 равных частей.

Даша хочет резать тортик по-научному, то есть вырезая куски из середины, а затем сдвигать оставшиеся части, чтобы тортик не засыхал.

На каком расстоянии от оси симметрии тортика (в долях от R) нужно проводить параллельные этой оси разрезы, чтобы первый кусок, отрезанный Дашей был симметричным относительно своих центральных осей и совпадал по объему с кусками, полученными у Маши?

Для решения трансцендентного уравнения построить график средствами Microsoft Excel.

Записать общий вид трансцендентного уравнения для случая разрезания тортика Машей на N частей.

Ответы

Vane12 12.02.2021 21:48

Так как тортики имеют постоянную высоту, то вместо рассмотрения объемов буем рассматривать соответствующие площади оснований.

Площадь основания тортика радиуса R:

$S=\pi R^2$

Тогда, площадь основания одного Машиного куска:

$S=\dfrac{\pi R^2}{8}$

Рассмотрим Дашин кусок (на картинке). Вертикальной и горизонтальной прямой разобьем его на 4 равные части и рассмотрим одну из них. Проведем еще одну прямую так, чтобы эта часть разделилась на сектор и прямоугольные треугольник.

Рассмотрим полученный сектор. Пусть α - угол между радиусами, образующими сектор. Тогда, площадь сектора:

$S_1=\dfrac{\pi R^2}{2\pi} \cdot \alpha$

Рассмотрим прямоугольный треугольник. Зная, что накрест лежащие углы при параллельных прямых равны, получим, что один из острых углов этого треугольника равен α. Выразим через этот угол и известный радиус катеты треугольника:

$\sin \alpha=\dfrac{d}{R} \Rightarrow d=R\sin \alpha$

$\cos \alpha=\dfrac{x}{R} \Rightarrow x=R\cos \alpha$

Площадь прямоугольного треугольника:

$S_2=\dfrac{dx}{2} =\dfrac{R\sin \alpha \cdot R\cos\alpha }{2} =\dfrac{R^2\sin \alpha \cos\alpha }{2}$

Тогда, запишем сумму, представляющую площадь основания четверти кусочка Даши:

$\dfrac{S}{4}=S_1+S_2=\dfrac{\pi R^2}{2\pi} \cdot \alpha+\dfrac{R^2\sin \alpha \cos\alpha }{2}$

Отсюда площадь основания кусочка Даши:

$S=\dfrac{4\pi R^2}{2\pi} \cdot \alpha+\dfrac{4R^2\sin \alpha \cos\alpha }{2}$

По условию куски Маши и Даши должны быть одинаковы. значит:

$\dfrac{\pi R^2}{8}=\dfrac{4\pi R^2}{2\pi} \cdot \alpha+\dfrac{4R^2\sin \alpha \cos\alpha }{2}$

$\dfrac{\pi}{8}=\dfrac{4\pi}{2\pi} \cdot \alpha+\dfrac{4\sin \alpha \cos\alpha }{2}$

$\dfrac{\pi}{8}=2\alpha+\sin2\alpha$

$2\alpha+\sin2\alpha=\dfrac{\pi}{8}$

$2\alpha+\sin2\alpha-\dfrac{\pi}{8}=0$

Для решения уравнения построим график в Microsoft Excel (картинка).

По графику определим, что равенство выполняется при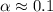 $\alpha \approx 0.1$ .

График при $x\to0$ напоминает прямую, так как в данном случае имеем место быть первый замечательный предел.

Действительно, можно считать, что рассматриваемый угол α мал. Тогда: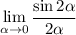 $\lim\limits_{\alpha \to0}\dfrac{\sin2\alpha }{2\alpha }$ в соответствии с первым замечательным пределом. Тогда от имеющегося уравнения можно перейти к более простому:

$2\alpha+\sin2\alpha-\dfrac{\pi}{8}=0$

$2\alpha+2\alpha-\dfrac{\pi}{8}\approx0$

$4\alpha\approx\dfrac{\pi}{8}$

$\alpha\approx\dfrac{\pi}{32}\approx0.098\approx0.1$

Искомое расстояние от оси симметрии соответствует уже вводившейся величине d:

$d=R\sin \alpha=R\sin 0.1$

По той же причине синус малого аргумента можно заменить самим этим аргументом. Получим:

$\boxed{d=0.1R}$

В частности, для практических целей выполненные приближенные допущения вполне допустимы и удачны.

Вернемся к полученному ранее уравнению:

$2\alpha+\sin2\alpha=\dfrac{\pi}{8}$

Заметим, что информация о том, что Маша разрезала свой тортик на 8 частей, сосредоточена в знаменателе правой части. Поэтому, если изначально Маша разрезала тортик на N частей, то проведя аналогичные рассуждения мы получим уравнение вида:

$\boxed{2\alpha+\sin2\alpha=\dfrac{\pi}{N}}$