если функция y=3x^2+ax-8 возрастает на промежутке [2;+00) и убывает на промежутке (-00; 2] то значение а ровно

ketgalyschko 2 07.03.2021 20:40 2

Question

Алгебра: если функция y=3x^2+ax-8 возрастает на промежутке [2;+00) и убывает на промежутке (-00; 2] то значение а ровно​

ketgalyschko · Answer

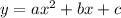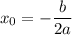Квадратичная функция задаётся формулой вида y = ax^2 + bx + c . То, что данная функция возрастает на промежутке $[2;+\infty)$ , а убывает на $(-\infty;\ 2]$ , означает, что абсцисса вершины параболы равна двум. Формула, по которой можно вычислить её: $x_0 = -\dfrac{b}{2a}$ (см. вид формулы). Тогда для функции 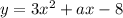y = 3x^2 + ax - 8 имеем: