Не просто решите, а объясните ход своих мыслей. просто решение мне не нужно.

Нам известен котангенс, а требуют найти тангенс. Попробуем преобразовать этот тангенс так, чтобы в нём встречался котангенс.

Что можно сделать с тангенсом суммы? Разложить по формуле:

Получили тангенсы, но двойного угла. Разложим их тоже:

Если сейчас заменить тангенсы на котангенсы, нам придётся работать с трёхэтажными дробями, поэтому лучше выразим тангенс из котангенса и будем подставлять: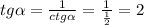

И теперь подставим двойку вместо тангенсов:

ответ: 5)

я бы делал так:

1) tg α*Ctg α = 1, ⇒ tg α = 2

2) tg2α = 2tgα/(1 - tg²α) = 4/(1 - 4) = -4/3

3) tg(2α + 5π/4) = (tg2α + tg5π/4)/(1 - tg2α*tg5π/4)

осталось подставить  все известные величины  и решить получившийся пример.

(-4/3 +1)/(1 +4/3*1) = -1/7