Найти область допустимых значений y=9x/(√9-x^2+√2x-5) 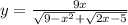
Другие вопросы по теме Алгебра
Популярные вопросы
- На тaці лежать пиріжки з м ясом із вишнями, до того ж пиріжків з м ясом...
2 - Пещеры на территории Казахстана...
2 - найти шестое слово о космосе. Это Сор ...
1 - Обчислити площу фігури обмежену лініями y=x²-4x+4; y-(7+20)x=0...
1 - Задано вектори а( -12; 8; 4) і б ( -1; 0; 2). Знайдіть координати вектора:...
3 - Переменка. Первый клас. Одгадайте ребус ! ...
3 - У якому регіоні було сконцентроване виробництво товарної пшениці...
3 - Різниця двох чисел дорівнює 15 а добуток 1000 знайдіть ці числа...
3 - Постав замість зірочок такі цифри, щоб число: 1) 3*5* ділилося на 9і на...
3 - Знайдіть координати вектора В(х, у), якщо (–1; 2), В(0 )....
2
найти область допустимых значений y=9x/(√9-x^2+√2x-5)
знаменатель не равен 0
√(9-x^2)+√(2x-5) ≠ 0
Сумма 2-х корней = 0, когда каждый равен 0
такого нет √(9-x^2)+√(2x-5) > 0
подкоренные выражения ≥ 0
9 - x² ≥ 0 -3 ≤ x ≤ 3
2x - 5 ≥ 0 x ≥ 2.5
ответ x∈ [2.5, 3]