1. Алгебра
  2. Найдите первый член и

Найдите первый член и знаменатель прогрессии, если известно, что b4-b2= - 45/32 и b6-b4 = - 45/512

Анастасия3342 Анастасия3342    2   03.06.2019 00:00    17

Ответы
olchik75 olchik75  01.10.2020 17:36

1) q =\frac{1}{4} ,b{_1}=6;\\\\2) q =-\frac{1}{4} ,b{_1}=-6.

Объяснение:

b{_4}-b{_2} =-\frac{45}{32} ; b{_6}-b{_4} =-\frac{45}{512} .

Воспользуемся формулой n-го члена геометрической прогрессии  и составим систему уравнений:

b{_n}=b{_1} *q^{n-1} ;\\\\\left \{ \begin{array}{lcl} {{b{_1} *q^{3} -b{_1}*q=-\frac{45}{32} ,} \\\\ {b{_1}* q^{5} -b{_1}* q^{3} =-\frac{45}{512}; }} \end{array} \right.\Leftrightarrow\left \{ \begin{array}{lcl} {{b{_1}*q*( q^{2}- 1)=-\frac{45}{32}, } \\\\ {b{_1} *q^{3} * (q^{2}-1) =-\frac{45}{512} .}} \end{array} \right.

Разделим почленно второе уравнение на первое и получим:

q^{2} = - \frac{45}{512} : (-\frac{45}{32} );\\\\q^{2} = \frac{32}{512} ;\\\\q^{2} =\frac{1}{16} ;\\\\\left [ \begin{array}{lcl} {{q=\frac{1}{4} ,} \\ \\{q=-\frac{1}{4} }} \end{array} \right.

Найдем первый член прогрессии

при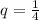  q=\frac{1}{4}

b{_1}* \frac{1}{4} *((\frac{1}{4} )^{2} -1)=-\frac{45}{32} ;\\\\b{_1}* \frac{1}{4} *(\frac{1}{16} -1)=-\frac{45}{32} ;\\\\b{_1}* \frac{1}{4} *(- \frac{15}{16} )=-\frac{45}{32} ;\\\\b{_1} *(- \frac{15}{64} )=-\frac{45}{32} ;\\\\b{_1} = -\frac{45}{32} :(-\frac{15}{64} );\\\\b{_1} =\frac{45*64}{32*15} ;\\\\b{_1}=6.

при q=-\frac{1}{4}

b{_1}* (-\frac{1}{4} )*((-\frac{1}{4} )^{2} -1)=-\frac{45}{32} ;\\\\b{_1}* (-\frac{1}{4} )*(\frac{1}{16} -1)=-\frac{45}{32} ;\\\\b{_1}* (-\frac{1}{4}) *(- \frac{15}{16} )=-\frac{45}{32} ;\\\\b{_1} * \frac{15}{64} =-\frac{45}{32} ;\\\\b{_1} = -\frac{45}{32} :\frac{15}{64} ;\\\\b{_1} =-\frac{45*64}{32*15} ;\\\\b{_1}=-6.

ПОКАЗАТЬ ОТВЕТЫ
Snzjxj Snzjxj  01.10.2020 17:36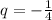

При имеющихся исходных данным возможно 2 ответа:

1) b₁ = 6; q = 1/4;

1) b₁ = -6; q = -1/4;

Объяснение:

Член геометрической прогрессии с номером n вычисляется по формуле

b_{n} = b_{1} \cdot q^{n-1}

b₄ - b₂ = b₁ · q³ - b₁· q  = b₁q(q² - 1)

b₆ - b₄ = b₁ · q⁵ - b₁· q³  = b₁q³(q² - 1)

По условию

b₁q(q² - 1) = -45/32    (1)

b₁q³(q² - 1) = -45/512    (2)

Преобразуем выражение (2)

b₁q³(q² - 1) = b₁q(q² - 1) · q²

В численном виде это можно записать как

-45/512 = -45/32 ·  q²

Откуда

q² = -45/512 : (-45/32)

q² = 1/16

q = ±1/4

Подставим q = 1/4 в выражение (1)

\dfrac{b_{1}}{4}\cdot \Big (\dfrac{1}{16} -1 \Big )= - \dfrac{45}{32}

\dfrac{b_{1}}{4}\cdot \Big (-\dfrac{15}{16} \Big )= - \dfrac{45}{32}

\dfrac{-15b_{1}}{64} = -\dfrac{45}{32}

0.5b₁ = 3

b₁ = 6

Подставим q = -1/4 в выражение (1)

-\dfrac{b_{1}}{4}\cdot \Big (\dfrac{1}{16}-1 \Big )= - \dfrac{45}{32}

-\dfrac{b_{1}}{4}\cdot \Big (-\dfrac{15}{16} \Big )= - \dfrac{45}{32}

\dfrac{15b_{1}}{64} = -\dfrac{45}{32}

0.5b₁ = -3

b₁ = -6

Проверка:

1) b₁ = 6; q = 1/4

b₂ = 6 ·  1/4 = 3/2

b₄ = 6 · 1/64 = 3/32

b₄ - b₂ = 3/32  - 3/2 = -45/32

b₆ = 6 ·  1/1024 = 3/512

b₆ - b₄ = 3/512  - 3/32 = -45/512

2) b₁ = -6; q = -1/4

b₂ = -6 ·  (-1/4) = 3/2

b₄ = -6 · (-1/64) = 3/32

b₄ - b₂ = 3/32  - 3/2 = -45/32

b₆ = -6 ·  (-1/1024) = 3/512

b₆ - b₄ = 3/512  - 3/32 = -45/512

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
thenotoriioussmma thenotoriioussmma  17.09.2019 15:10
Велосипедист ехал 2ч по лесной дороге и 1 ч по шоссе .всего проехал 40 км .и по шоссе на 4 км /ч его скорость больше ,чем по лесной дороге .с какой скоростью велосипедист...
KseniaДьявол KseniaДьявол  17.09.2019 15:10
A1 найдите сумму многочленов 2 2 -5y-9 и 7y-y+1. a2 выражение 3 3 2 (2-+2x+5x)+(x-x) a3 найдите значение выражения 2 (8,1xy-3y)+(7,1y2x+x) при x=-3,5 и y=1 a3 решите...
kateshaginian kateshaginian  17.09.2019 15:10
Установить область определения функций f(x)=√4-log2(x+1) !...
0ananasik0 0ananasik0  17.09.2019 15:10
Последовательности заданы несколькими первыми членами. одна из них-арифметическая прогрессия. укажите её 1) 6; 7; 9; 12; 2)2; 4; 8; 16; 3)2; 4; 6; 8; 4)3; 1; 1/3;...
лена062 лена062  17.09.2019 15:10
Велосипедист ехал по лесной дороге 2 часа и час по шоссе . всего проехал 40 км.и по шоссе скорость на 4 км больше, чем по лесной дороге.с какой скорость велосипедист...
kimas98 kimas98  11.09.2019 20:40
Решить неравенства: 1) arcsin(2-3x)=р/6 2) arcsin x-2/4=-p/4 3) arcsin(3-2x)=p/4 4) arcsin x+3/2=-p/3 5)arccos(2x+3)=p/4 6)arccos x+1/3=2p/3 7)arccos (3x+1)=p/2...
Александр12345678911 Александр12345678911  11.09.2019 20:40
Решить систему методом подстановки: а) 2x-y=4; x+2y=7, б) 3x-y=-4; -5x+2y=-1...
Maxi2007 Maxi2007  11.09.2019 20:40
Решите уравнение: а) х²+3х-1+√х²+3х-9 = 0 б) х²+2х-11+√х²+2х-1 = 0 выражения √х²+3х-9 и √х²+2х-1 под корнем...
sweetmalboro sweetmalboro  11.09.2019 20:40
Чему равно минус 1 во второй степени...
olgalubnina201 olgalubnina201  11.09.2019 20:40
Вынесите за скобки общий множитель: (x квадрат +3x)квадрат; x в 3n+2 степени + x в n степени,где n натуральное число...

Популярные вопросы