Найдите наименьшее натуральное число n, для которого < {√n}< здесь {√n} - дробная часть числа √n.

Рассмотрим числа между числами k² и (k+1)²; Этих чисел ровно 2k;

Разобъем расстояние между этими числами на ячейки и пронумеруем их от i=1 до i=2k; Тогда дробная часть корня от i-того элемента не превосходит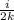  ; Рассматривая данные верхнее и нижнее ограничение, приходим к другой задаче: найти такое наименьшее значение k, при котором выполнено неравенство: 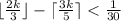; Небольшим перебором выходим на число k=3; Значит искомое n лежит в промежутке [9;16];

Здесь сразу видно, что n=11