Найдите наибольшее значение функции y = (27 − x)√x на отрезке [1; 16]

y наиб = у max = 54

Объяснение:

Дана функция y= (27 - x) · √x

Производная этой функции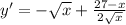

Упростим это выражение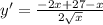

х ≠ 0 , но этот разрыв  производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]

y' = 0

(27 - 3x) = 0

Точка экстремума одна x = 9.

При х < 9   y' > 0; при х > 9    y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.

у наиб = у max = y(9) = (27 - 9) · √ 9 = 54