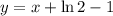Написать уравнение касательной к графику функци y=ln(1+x^2) в точке с абсциссой, равной 1. сделать чертёж.
Другие вопросы по теме Алгебра
Популярные вопросы
- Прохождения световых лучей через оптическую структуру...
2 - Составить содержательные предложения со словами: - контакт - щелкун -...
1 - Прилагательное заканчивается на ами ?...
1 - Осевое сечение цилиндра - квадрат, длина диагонали которого равна 36см....
2 - 8класс. тема: подобные треугольники. площади подобных треугольников равны...
3 - По какому правилу составлена таблица надо продолжить 86 76 66 56 46 еще...
3 - :в трёх классах всего 83 ученика. в первом классе учатся 5/6 от количества...
3 - Какие показатели определяют границы биосферы: а)микроорганизмы и продукты...
2 - На пасхе было 7 полных7наполовину наполненных мёдом и 7 пустых бочонков...
2 - Жители страны любят устраивать различные соревнования. два треугольника...
2
Уравнение касательной: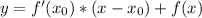
Найдём производную сложной функции по правилу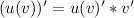 , где
, где 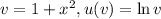
Уравнение касательной в точке x = 1: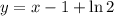
ответ: