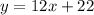Написать уравнение касательной графику функции 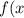 = {x}^{3} + 6) проходящей через точку с абсциссой -2
проходящей через точку с абсциссой -2
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто автор этого произведения? снег идет, густой-густой. снег, как с яблонь, лепестками....
2 - 6речень з дієприслівниковим зворотом...
1 - Кто писал под пвсевдонимом марк твен или чарльз диккенс...
1 - Собери пословицы.з частей 1. что посеешь / а). плесенью покрывается 2.жизнь прожить....
2 - |2x-5|=9 |0,6+x|=7 |0,4x-1|=2 |2,5x-3|=7 решить уравнение заранее...
2 - Что значит тригонометрическое уравнение к простейшему виду? по например :...
1 - Почему птицы не едят бабочек-геликонид?...
1 - Составить 6 предложений со сложносочиненными союзами либо,или,то-то....
3 - Придумати історію н аглійській мові на п ятнадцять речень...
3 - Врезультате дробления зиготы образуется...
1
y=12x+22
Объяснение:
Уравнение касательной: y=f(a)+f′(a)(x-a), где a-точка касания.
1.f(a)=f(-2)=-8+6=-2
2.f'(x)=3x²
3.f'(a)=3*4=12
y=-2+12(x+2)=-2+12x+24=12x+22
Уравнение касательной имеет вид:
Определим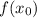 :
:
Найдем производную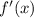
Определим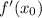 :
:
Теперь определим уравнение касательной:
ответ: