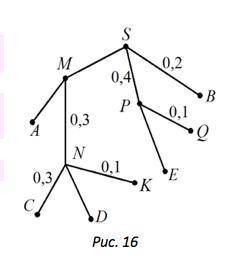
На рисунке 16 изображено дерево некоторого случайного эксперимента с началом в точке .
а) Изобразите дерево в своей тетради и напишите недостающие вероятности на рёбрах.
б) Сколько в этом случайном эксперименте элементарных событий?
в) Найдите вероятность цепочки .
г) Найдите вероятность события .
Ответы
Добрый день! Давайте рассмотрим задачу по порядку.
а) Чтобы изобразить дерево в тетради и написать недостающие вероятности на ребрах, нам нужно пронумеровать вершины и ребра дерева. Давайте нумерацию вершин проведем по строкам от верхней до нижней, а ребра будем нумеровать по порядку.
1. В начале есть одна вершина без входящих ребер, ее обозначим как V1.
2. Из этой вершины (V1) идут два ребра, которые обозначим как E1 и E2. Пусть E1 соединяет V1 с V2, а E2 - с V3.
3. Из V2 идут два новых ребра, которые обозначим как E3 и E4. Пусть E3 соединяет V2 с V4, а E4 - с V5.
4. Аналогично, из V3 идут два новых ребра, которые обозначим как E5 и E6. Пусть E5 соединяет V3 с V6, а E6 - с V7.
Итак, наше дерево будет выглядеть следующим образом:
```
V1
↙ ↘
E1 E2
↙ ↘ ↙ ↘
V2 V3 V4 V5
↙ ↘ ↘
E3 E4 E5 E6
↙ ↘
V4 V5
```
Теперь можно заполнить недостающие вероятности на ребрах:
- Вероятность пути, соответствующего ребру E1, обозначим как P(E1).
- Вероятность пути, соответствующего ребру E2, обозначим как P(E2).
- Вероятность пути, соответствующего ребру E3, обозначим как P(E3).
- Вероятность пути, соответствующего ребру E4, обозначим как P(E4).
- Вероятность пути, соответствующего ребру E5, обозначим как P(E5).
- Вероятность пути, соответствующего ребру E6, обозначим как P(E6).
б) Элементарные события - это те, которые происходят в самом нижнем слое дерева. В данном случае, это V4, V5, V6 и V7.
Итак, в данном случайном эксперименте 4 элементарных события.
в) Найдем вероятность цепочки A:
A = V1 → V2 → V4
Чтобы найти вероятность цепочки A, нужно перемножить вероятности соответствующих ребер:
P(A) = P(E1) * P(E3)
г) Найдем вероятность события B:
B = V1 → V3 → V6
Чтобы найти вероятность события B, нужно перемножить вероятности соответствующих ребер:
P(B) = P(E2) * P(E5)
Надеюсь, объяснение понятно и поможет вам решить задачу. Если остались вопросы, пожалуйста, задайте их.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Ак вы понимаете смысл фразы человек твёрд семьёй...
2 - Мальчики поймали три рыбы массой 3кг150г.две рыбы были одинаковой...
3 - На подготовку учащийся потратил две целых две-третьих часа.из них...
2 - Нужна ! самолёт летит горизонтально со скоростью 1600км/ч. почему...
1 - Какие грамматические признаки можно определить у слова болеть...
3 - Опеределить объём газа, который выделится при взаимодействии азотной...
1 - Масса восьми одинаковых коробок с пастилой неженка равна 4800 г.чему...
1 - Как изменится период колебаний груза на пружине если масса груза...
2 - Стоимость автомобиля с гаражом состовляет 355600руб. сколько стоит...
2 - 1. написать программу вычисления площади кольца, где исходными данными...
1