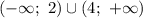Иследоовать функцию на монотонность и экстремум! y'=(x^3-9x^2+24x-12
Другие вопросы по теме Алгебра
Популярные вопросы
- ГОСПОДИ КТО ПОИОЖЕТ,ТЫ САМЫЙ СВЯТОЙ ЧЕЛОВЕК...
2 -  взаимно-обратная дробь 7/10...
2 - ДОМАШНЕЕ ЗАДАНИЕ Реши задачу.ЖПОЧЕМУНАЗОВИОБЪЯСНИСостанции одновременно...
1 - кто просто так в ответ напишет комент того бан. А если ответ правильный...
3 - Определите высоту над Землей, где сила тяготения уменьшилась на...
1 - Рыцарские поэты Северной Франции, Италии, Испании и Германии...
1 - ТОЛЬКО У МЕНЯ СОЧ ОТВЕТЬТЕ С РЕШЕНИЕМ И ПРАВЕЛЬНО РАСКРОЙ СКОБКИ...
1 - Яку масу дибромопропану можна добути з 8,96 л пропену...
3 - Описание И.И.Шишкина дорога в лесу...
1 - Чего же боялся фриц из повести Щелкунчик и мышиный король...
3
y=x^3-9x^2+24x-12
y'=(x^3-9x^2+24x-12)'=3x^2-18x+24
y'=0
x^2-6x+8=0
x1=2 x2=4
y'(0)=24>0
y'(3)=3*3^2-18*3+24=-3<0
y'(5)=3*5^2-18*5+24=90>0
y_(min)=y(4)=4^3-9*4^2+24*4-12=64-144+96-12=4
y_(max)=y(2)=2^3-9*2^2+24*2-12=8-36+48-12=8
Точка минимума (4; 4)
Точка максимума (2; 8)
Функция убывает на промежутке (2; 4)
Функция возрастает на промежутках