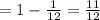Игральный кубик бросили два раза. найдите вероятность того, что: а) среди выпавших чисел есть хотябы одна единица; б) сумма выпавших чисел не больше 3; в) сумма выпавших чисел меньше 11; г) произведение выпавших чисел меньше 27.

Во всех пунктах у нас имеется n = 6*6 = 36 исходов.

a) Исходов содержащих единицу у нас m = 11:

(1,1)

(1,2),(2,1)

(1,3),(3,1)

(1,4),(4,1)

(1,5),(5,1)

(1,6),(6,1)

b) Т.е. сумма 2 или 3 (1 быть не может). Всего три положительных исхода:

(1,1), (1,2), (2,1). m = 3

c) 11 = 6+5, 11 = 5+6, 12 = 6+6, m = 3

p(сумма чисел меньше 11) = 1 - p(сумма чисел больше или равна 11)

p(сумма чисел больше или равна 11)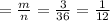

p(сумма чисел меньше 11)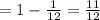

d)

p(произведение чисел меньше 27) = 1 - p(произведение чисел больше или равно 27)

6*6 = 36

6*5 = 5*6 = 30

5*5 = 25, 6*4 = 24 - не подходят. m = 3

p(произведение чисел больше или равно 27)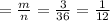

p(произведение чисел меньше 27)