Хэлп! Меня интересует очень подробное решение двух уравнений, чтобы понять. Как можно подробнее, с пояснениями, какую формулу используете и как понять какую именно надо. Ну, тоесть все детали должны быть написаны. Заранее ответ не в тему=нарушение

Ответы

TheBrainPlay 11.10.2020 20:12

Воспользуемся методом вс угла.

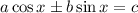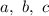Рассмотрим уравнение вида $a\cos x \pm b\sin x = c$ , где $a, \ b, \ c$ — коэффициенты,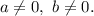 $a \neq 0, \ b \neq 0.$

Разделим обе части этого уравнения на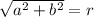 $\sqrt{a^{2} + b^{2}} = r$

Получим:

$\dfrac{a}{r} \cos x \pm \dfrac{b}{r}\sin x = \dfrac{c}{r}$

Коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль каждого из них не превосходит единицы, а сумма их квадратов равна 1.

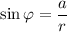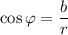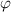Тогда можно обозначить их соответственно $\sin \varphi = \dfrac{a}{r}$ и $\cos \varphi = \dfrac{b}{r}$ (здесь $\varphi$ — вс угол) и уравнение примет вид:

$\sin \varphi \cos x \pm \cos \varphi \sin x = \dfrac{c}{r}$

Из формулы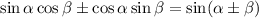 $\sin \alpha \cos \beta \pm \cos \alpha \sin \beta = \sin (\alpha \pm \beta )$ имеем:

$\sin (\varphi \pm x) = \dfrac{c}{r}$

Решим уравнения:

$1) \ \dfrac{\sqrt{3}}{2}\cos x - \dfrac{1}{2} \sin x = 1$

$\cos \dfrac{\pi}{6} \cos x - \sin \dfrac{\pi}{6}\sin x = 1$

Воспользуемся формулой косинуса суммы / разности:

$\cos \alpha \cos \beta \pm \sin \alpha \sin \beta = \cos (\alpha \mp \beta )$

Имеем:

$\cos \left(\dfrac{\pi}{6} + x \right) = 1$

$\dfrac{\pi}{6} + x = 2\pi n, \ n \in Z$

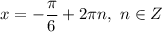
$x = -\dfrac{\pi}{6} + 2\pi n, \ n \in Z$

ответ: $x = -\dfrac{\pi}{6} + 2\pi n, \ n \in Z$

$2) \ \sqrt{3}\cos x + \sin x = 1 \ \ \ | : \sqrt{(\sqrt{3})^{2} + 1^{2}}$

$\dfrac{\sqrt{3}}{2}\cos x + \dfrac{1}{2} \sin x = \dfrac{1}{2}$

$\sin \dfrac{\pi}{3}\cos x + \cos \dfrac{\pi}{3}\sin x = \dfrac{1}{2}$

Воспользуемся формулой синуса суммы / разности:

$\sin \alpha \cos \beta \pm \cos \alpha \sin \beta = \sin (\alpha \pm \beta )$

Имеем:

$\sin \left(\dfrac{\pi}{3} + x \right) = \dfrac{1}{2}$

$\dfrac{\pi}{3} + x = (-1)^{n}\arcsin \dfrac{1}{2} + \pi n, \ n \in Z$

$\dfrac{\pi}{3} + x = (-1)^{n}\dfrac{\pi}{6} + \pi n, \ n \in Z$

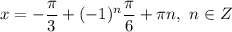
$x = -\dfrac{\pi}{3} + (-1)^{n}\dfrac{\pi}{6} + \pi n, \ n \in Z$

ответ: $x = -\dfrac{\pi}{3} + (-1)^{n}\dfrac{\pi}{6} + \pi n, \ n \in Z$

Примечание. Выбор формулы сложения для синуса или косинуса не является принципиальным. Здесь для удобства выбраны формулы именно такие, чтобы под тригонометрической функцией стоял аргумент со знаком плюс. Можно непосредственно пользоваться формулой для решения такого рода уравнений.

Второй метод: универсальная тригонометрическая подстановка.

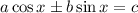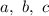Для уравнений вида $a\cos x \pm b\sin x = c$ , где $a, \ b, \ c$ — коэффициенты, 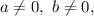$a \neq 0, \ b \neq 0,$ воспользуемся выражениями тригонометрических функций через тангенс половинного аргумента:

$\sin \alpha = \dfrac{2\text{tg} \ \dfrac{\alpha }{2} }{1 + \text{tg}^{2} \ \dfrac{\alpha }{2} }$

$\cos \alpha = \dfrac{1 - \text{tg}^{2} \ \dfrac{\alpha }{2} }{1 + \text{tg}^{2} \ \dfrac{\alpha }{2} }$

Перепишем уравнение:

$a \cdot \dfrac{1 - \text{tg}^{2} \ \dfrac{x}{2} }{1 + \text{tg}^{2} \ \dfrac{x}{2} } \pm b\cdot \dfrac{2\text{tg} \ \dfrac{x }{2} }{1 + \text{tg}^{2} \ \dfrac{x}{2} } = c$

Сделаем соответствующую замену: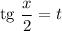 $\text{tg} \ \dfrac{x}{2} = t$

Получили уравнение:

$a \cdot \dfrac{1 - t^{2} }{1 + t^{2} } \pm b \cdot \dfrac{2t}{1 + t^{2} } = c$

После решения данного уравнения (обычно, их 2) следует вернутся к замене и получить решения:

$x = 2 \, \text{arctg} \, t + 2\pi n, \ n \in Z$

Для заданных уравнений более рациональным является первый метод решения, потому что их не сложно свести к уравнению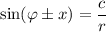 $\sin (\varphi \pm x) = \dfrac{c}{r}$ , а процедура выискивания корней дробно-рационального уравнения для второго метода — это еще один относительно большой шаг для решения такого рода уравнений.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра