докажите что данное уравнение является уравнением сферы x^2+y^2+z^2+4y-6z+5=0
10-
Другие вопросы по теме Алгебра
Популярные вопросы
- Многоцветная радуга висела над лугом, яркое солнце блестело на спинах бодро бежавших...
1 - На стороне ВС прямоугольника ABCD взята точка М так, что АМ=13 см, АВ=12 см,...
1 - дать название веществам до завтра надо....
2 - Выразите в сантиметрах 3/10 m...
3 - Напиши рассказ о футболе (5-7 предложений ) используй слова с НЕ и НИ в качестве...
1 - Написать эссе по повести «Один день Ивана Денисовича»...
2 - Дополните предложения предложенными словами. 1. Между определёнными видами деревьев...
3 - решить! алгебра 7 класс. а(а-2)-(а-1)(а+1) и уравнение (х-5)(2х...
2 - Матем 108 бет.Жиындардың элементтерін ата ...
3 - сделать анализ стикотворения . Отъезд Забудутся ссоры, отъезды, письма. Мы умрём,...
1
Уравнение сферы с центром в точке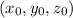 и радиусом R имеет вид:
и радиусом R имеет вид:
Уравнение сферы в общем виде
(х-а)²+(у-b)²+(z-c)²=R²,где (а;b;с)-центр сферы, R- ее радиус.
x²+(y-2)²-4+(z-3)²-9+5=0
x²+(y+2)²-4+(z-3)²-9+5=0
x²+(y+2)²+(z-3)²=8 - сфера с центром в точке (0;-2;3), и радиусом, равным √8=2√2
Доказано.