Дифференциальная уравнения! 3.10

Question

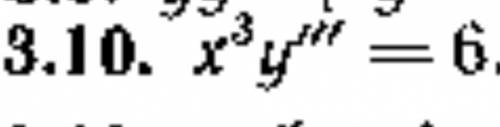
Алгебра: Дифференциальная уравнения! 3.10

LogiutNowakk · Answer

y(x) = 3log(x) + C1*x²/2 + C2*x + C3 (C1, C2, C3 - константы)

Объяснение:

x³ * y''' = 6

Запишем это как x³ *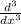 $\frac{d^3}{dx^3}$ * y(x) = 6

$\frac{d^3}{dx^3}$ * y(x) = 6/x³

Начнем интегрировать.

$\frac{d^2 y(x)}{dx^2}$ = ∫ 6/x³ dx = -3/x²+ C1 (C1 - константа)

$\frac{d y(x)}{dx}$ = ∫ (-3/x² + C1) dx = 3/x + C1x + C2 (C2 - константа)

y(x) = ∫ (3/x + C1x + C2) dx = 3log(x) + C1x²/2 + C2x + C3 (C3 - константа)