Дан равностороний треугольник со стороной 8 см из его высот построен второй треугольник а из высот второго третий и.т.д докажите что периметры

Question

Алгебра: Дан равностороний треугольник со стороной 8 см из его высот построен второй треугольник а из высот второго третий и.т.д докажите что периметры треугольников образуют прогрессию и найдите периметр шестого тнреугольника

Xaby · Answer

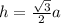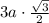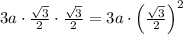Высота равностороннего тр-ка рассчитывается по формуле $h=\frac{\sqrt3}2a$ , где a - сторона тр-ка. Периметр первого тр-ка 3a, периметр второго тр-ка $3a\cdot\frac{\sqrt3}2$ , периметр третьего $3a\cdot\frac{\sqrt3}2\cdot\frac{\sqrt3}2=3a\cdot\left(\frac{\sqrt3}2\right)^2$ .

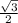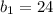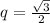Получеатся, что периметр каждого последующего тр-ка равен периметру предыдущего, умноженному на постоянный множитель $\frac{\sqrt3}2$ . Относительно периметров имеем геометрическуй прогрессию с первым членом b_1=24 и знаменателем $q=\frac{\sqrt3}2$ .