Алгебра: Abcd – квадрат. равны ли векторы: а) ва и dc; б) вс и ad; в) da и dc?

Решение:Рисунок смотрите в приложении (на нем изображены равные векторы).Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).а). Векторы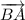 и равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен 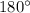градусов (получаем, что это коллинеарные, но не равные векторы)..б). Векторы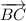 и равны по длине, лежат на параллельных прямых и имеют одинаковое...

Abcd – квадрат. равны ли векторы: а) ва и dc; б) вс и ad; в) da и dc?

Ответы

рвржвжчржч 08.10.2020 23:44

Решение:

Рисунок смотрите в приложении (на нем изображены равные векторы).

Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).

а). Векторы $\overrightarrow{BA}$ и $\overrightarrow{DC}$ равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен $180 ^\circ$ градусов (получаем, что это коллинеарные, но не равные векторы).

$\overrightarrow{BA} \neq \overrightarrow{DC}$ .

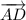б). Векторы $\overrightarrow{BC}$ и $\overrightarrow{AD}$ равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.

$\overrightarrow{BC} = \overrightarrow{AD}$ .

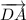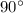в). Векторы $\overrightarrow{DA}$ и $\overrightarrow{DC}$ опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - $90^\circ$ градусов).

$\overrightarrow{DA} \neq \overrightarrow{DC}$

ответ:

а) нет;

б) да;

в) нет.

Abcd – квадрат. равны ли векторы: а) ва и dc; б) вс и ad; в) da и dc?

ПОКАЗАТЬ ОТВЕТЫ

dzeratigieva 19.01.2024 11:03

Добрый день! Я буду вам помогать в роли учителя. Давайте разберемся с каждым пунктом по очереди.

а) Векторы ва и dc - это векторы, которые указывают направление и длину отрезков в квадрате Abcd. Чтобы выяснить, равны ли эти векторы, нам нужно сравнить их значения.

Рассмотрим первый вектор va. Он указывает направление и длину отрезка, идущего от вершины A до вершины B.
Теперь рассмотрим вектор dc. Он указывает направление и длину отрезка, идущего от вершины D до вершины C.

Чтобы понять, равны ли эти векторы, сравним значения координат их начальной и конечной точек.

Начальная точка вектора va - это точка A, а конечная точка - это точка B.
Начальная точка вектора dc - это точка D, а конечная точка - это точка C.

Если значения координат начальных и конечных точек обоих векторов одинаковы, то это значит, что длина и направление этих векторов одинаковы и они равны. Давайте проверим:

Координаты точки A: (xA, yA)
Координаты точки B: (xB, yB)
Координаты точки D: (xD, yD)
Координаты точки C: (xC, yC)

Сравним значения координат:
xA = xD и yA = yD (координаты начальных точек совпадают)

xB = xC и yB = yC (координаты конечных точек совпадают)

Таким образом, значения координат начальных и конечных точек обоих векторов совпадают, а значит, вектора va и dc равны.

б) Теперь рассмотрим векторы вс и ad. Аналогично предыдущему пункту, нам нужно сравнить значения координат их начальных и конечных точек.

Начальная точка вектора вс - это точка A, а конечная точка - это точка C.
Начальная точка вектора ad - это точка A, а конечная точка - это точка D.

Сравним значения координат:
xA = xA и yA = yA (координаты начальных точек совпадают)

xC ≠ xD или yC ≠ yD (координаты конечных точек не совпадают)

Поскольку значения координат конечных точек векторов вс и ad не совпадают, значит, эти векторы не равны.

в) Наконец, рассмотрим векторы da и dc. Опять же, сравним значения координат их начальных и конечных точек.

Начальная точка вектора da - это точка D, а конечная точка - это точка A.
Начальная точка вектора dc - это точка D, а конечная точка - это точка C.

Сравним значения координат:
xD = xD и yD = yD (координаты начальных точек совпадают)

xA ≠ xC или yA ≠ yC (координаты конечных точек не совпадают)

Поскольку значения координат конечных точек векторов da и dc не совпадают, значит, эти векторы не равны.

Итак, чтобы подвести итог:
а) Векторы va и dc равны.
б) Векторы вс и ad не равны.
в) Векторы da и dc не равны.

Я надеюсь, что мой ответ был понятен и полезен для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра