529.Найдите прoизвoдную от функции 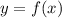 , когда a)
, когда a)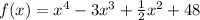
b)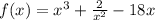
Другие вопросы по теме Алгебра
Популярные вопросы
- Чим повинні бути обладнані проходи нахилом більше 20°...
3 - В ательє шиють 2 види піджаків, 4 види блузок та та 3 види спідниць. Скільки...
2 - Қархан қай жерде жерленген? ...
1 - Вычислите: 1) 4. 13 - 25; 3) 4. 24. 5, 2) 125 - 17 - 8, 4) 50 - 236 - 2....
1 - Используя программу Microsoft Power Point, подготовь презентацию одного...
2 - План анализ стихотворения утес по плану:1.история создания2.тема3.основная...
2 - упростить. Можно просто ответ...
1 - Выполните тестовые задания.Тест по теме «Н и НН в суффиксах имен прилагательных»1....
3 - ОТВЕТИТЬ 1. Почему Наполеон объявил об установлении континентальной блокады...
3 - Черная курица,или Подземные жители. Написать отзыв о сказке: что понравилось...
3
Объяснение: