4. Найти производную функции 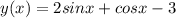 5. Решить тригонометрическое уравнение
5. Решить тригонометрическое уравнение 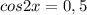
6. Найти корень уравнения 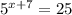
7. Решить неравенство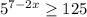
Другие вопросы по теме Алгебра
Популярные вопросы
- Описание басни бородино , надо!...
1 - Поиогите ! как правильно писать? ! скожите сколько сейчас времини? или...
2 - Вычислить массовую долю хлора в молекуле бертолетовой соли kclo3....
1 - Ссобачкой и саквояжем весят- 98 кг. саквояж весит 16 кг, а собачка 2...
2 - Создайте со словами шофер и ромашка предложения в ( и. п) и ( в. п)...
1 - Слово трепет разобрать как часть речи...
1 - (х²-1)√5х-1=0 решить уравнение (где 5х -все под корнем)...
1 - 1. найдите значение степени: две целых три четвертых во второй степени....
1 - Выражения и вычислите его значения при указанном значении буквы 1)34х+66х,если...
3 - Запиши вычисления столбиком. 35 км 820 м -7 км 900 м 1 ч 26 мин + 2 ч...
2
Объяснение:
4)
5)
6)
7)