1. Алгебра
  2. Обратите число в обыкновенную

Обратите число в обыкновенную дробь: 1)0,2(3); 2)1,(81); 3)0,32(45); 4) 1,6(3201)"

6frm129 6frm129    2   01.07.2019 23:50    1

Ответы
Анна157211цаа Анна157211цаа  26.07.2020 09:26

1).

\displaystyle 0,2(3)=0,2+0,0(3)=\frac{2}{10} +\frac{3}{90} = \frac{18+3}{90}= \frac{21}{90} = \boxed {\frac{7}{30} }

2).

\displaystyle 1,(81)=1+\frac{81}{99} = 1+\frac{9}{11} = \boxed{1\frac{9}{11}}

3).

\displaystyle 0,32(45)=0,32+0,00(45)=\frac{32}{100} +\frac{45}{9900} = \frac{3168+45}{9900} = \frac{3213}{9900} = \boxed{\frac{357}{1100}}

4).

\displaystyle 1,6(3201)=1+0,6+0,0(3201)=1+\frac{6}{10} +\frac{3201}{99990} = {1} \frac{59994+3201}{99990} = \\= 1\frac{63195}{99990} = \boxed{1\frac{383}{606}}

ПОКАЗАТЬ ОТВЕТЫ
zzzXXXD zzzXXXD  26.07.2020 09:26

Приведу другой через геометрическую прогрессию)

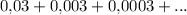0{,}2(3)=0{,}2+0{,}03+0{,}003+0{,}0003+...~\boxed{=}

Сумма 0{,}03+0{,}003+0{,}0003+... это сумма бесконечно убывающей геометрической прогрессии. Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле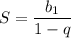 S=\dfrac{b_1}{1-q}

\boxed{=}~0{,}2+\dfrac{0{,}03}{1-0{,}1}=0{,}2+\dfrac{0{,}03}{0{,}9}=\dfrac{1}{5}+\dfrac{1}{30}=\dfrac{7}{30}

ответ: 7/30.

1{,}(81)=1+0{,}81+0{,}0081+0{,}000081+...~\boxed{=}

Бесконечно убывающая геометрическая прогрессия с первым членом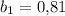 b_1=0{,}81 и знаменателем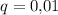 q=0{,}01

\boxed{=}~ 1+\dfrac{0{,}81}{1-0{,}01}=1+\dfrac{0{,}81}{0{,}99}=1+\dfrac{9}{11}=\dfrac{20}{11}

ответ: 20/11.

0{,}32(45)=0{,}32+0{,}0045+0{,}000045+0{,}00000045+...~\boxed{=}

Имеем бесконечно убывающую геометрическому прогрессию с первым членом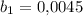 b_1=0{,}0045 и знаменателем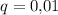 q=0{,}01

\boxed{=}~ 0{,}32+\dfrac{0{,}0045}{0{,}99}=0{,}32+\dfrac{5}{1100}=\dfrac{357}{1100}

ответ: 357/1100.

1{,}6(3201)=1{,}6+0{,}03201+0{,}000003201+...~\boxed{=}

Видим сумму бесконечно убывающей геометрической прогрессии с первым членом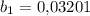 b_1=0{,}03201 и знаменателем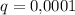 q=0{,}0001

\boxed{=}~1{,}6+\dfrac{0{,}03201}{1-0{,}0001}=1{,}6+\dfrac{0{,}03201}{0{,}9999}=1{,}6+\dfrac{3201}{99990}=\dfrac{989}{606}

ответ: 989/606.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Алёна0Чан Алёна0Чан  30.08.2019 01:20
Какая из точек принадлежит графику функции у = 5х-х^2 а) в (2; 6) б) а (-2; 6) в) с (-2; 14) г) d (-2; -14)...
olgaversh olgaversh  30.08.2019 01:20
Надо решить чему равен знамениты прогрессии (bn), если b12=–8 b13=14...
dsokolovskiyp015em dsokolovskiyp015em  30.08.2019 01:20
Вычислите производную функцию f(x)=(x^2)/(x+2) в точке х=-4...
asikg27 asikg27  30.08.2019 01:20
2·(х/2+у/4)² + (2х-у)² , , выражение. если можно-подробно по пунктам...
Sadist702 Sadist702  05.12.2020 09:46
Установите соответствие между функциями и их графиками. ​...
Prls Prls  05.12.2020 09:45
не понимаю как Решите систему уравнений графическим x+y=2 2x-y=7...
0оМорковкао0 0оМорковкао0  05.12.2020 09:45
Найди числовое значение многочлена, предварительно упростив его: Задание на фото...
Katukina Katukina  30.04.2021 09:36
решить системы неравенств:...
mikerinavera mikerinavera  30.04.2021 09:36
Сколько решений имеет система? : x+y=2;{ 3x-2y=11​...
MEhelpYOU MEhelpYOU  30.04.2021 09:36
Який розв язок має система рівнянь?...

Популярные вопросы