● 3. Представьте выражение
в виде степени с основанием
4. Сократите дробь:
а)
б)
![\sqrt[3]{ {a}^{5} } \times {a} ^{ - \frac {2}{3} }](/tpl/images/4367/2954/c4fbc.png)

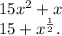
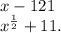
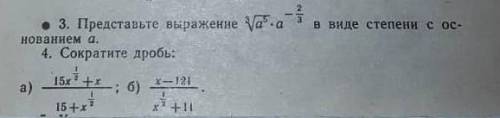
Другие вопросы по теме Алгебра
Популярные вопросы
- Мне нужен ответ по 6класс как это решили? 7 1/4+4 5/6=12 7/12...
2 - Как доказать наличие аминогруппы в a-положении?...
3 - Согласно программе северного общества декабристов, в россии должна...
2 - Зайку бросила хозяйка под дождем остался зайка весь до ниточки...
1 - Породы собак в рассказе постойко мамин-сибиряк...
2 - 1) определить энергию кванта, который имеет частоту 6*10^14 гц....
1 - Втрёх пробирках находятся: глицерин,уксусный альдегид,фенол.как...
1 - Расположите в хронологическом порядке а)основание индийского...
1 - Как углерод, так и калий реагируют с 1) оксидом натрия 2) алюминием...
3 - Первый рабочий может выкопать канаву за 2 часа а второй за 4...
2
Объяснение:
3)
4)
а)
б)
Объяснение: