Найдите все значения а, при которых уравнение |x+3|-1=|2x-a| имеет бесконечное множество решений? Единственное решение?

Ответы

Малинка1232 06.07.2021 13:46

(см. объяснение)

Объяснение:

$|x+3|-1=|2x-a|\\|2x-a|-|x+3|+1=0$

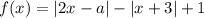Пусть f(x)=|2x-a|-|x+3|+1 .

Тогда нужно, чтобы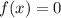 f(x)=0 имело единственное решение.

Заметим, что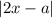 |2x-a| играет решающую роль в определении поведения функции (ее возрастания/убывания). Если он открывается со знаком +, то функция возрастает, иначе убывает.

Тогда промежуток убывания: $\left(-\infty;\;\dfrac{a}{2}\right]$ .

Промежуток возрастания: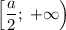 $\left[\dfrac{a}{2};\;+\infty\right)$ .

Единственное решение будет, если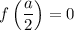 $f\left(\dfrac{a}{2}\right)=0$ .

Получили уравнение:

$\left|2\times\dfrac{a}{2}-a\right|-\left|\dfrac{a}{2}+3\right|+1=0,\;\;\left[\begin{array}{ccc}a=-4\\a=-8\end{array}\right;$

Значит при данных значениях параметра a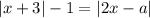 |x+3|-1=|2x-a| имеет единственное решение.

Бесконечное множество решений будет, если левая и правая части совпадают (то есть графики наложатся). Но это невозможно, так как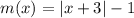 m(x)=|x+3|-1 более широкий (прямой угол), чем 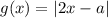g(x)=|2x-a| (острый угол) и величина угла от параметра никак не зависит.

Задание выполнено!

Комментарий:

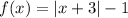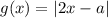Можно было решать задачу, строя f(x)=|x+3|-1 и g(x)=|2x-a| . Первый график имеет фиксированное положение, а второй бегает влево-вправо. Тогда тоже легко сделать требуемый вывод.