№10. Укажите промежуток, которому принадлежит корень уравнения 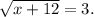$\sqrt{x+12}=3.$ А) [-12; -6);
Б) [-6; 0);
В) [0; 6);
Г) [6; 12);
Д) [12; +∞).

Question

Алгебра: №10. Укажите промежуток, которому принадлежит корень уравнения А) [-12; -6); Б) [-6; 0); В) [0; 6); Г) [6; 12); Д) [12; +∞).

ElenaDzaraxova · Answer

БОбъяснение:По определению арифметического квадратного корняКорень -3 принадлежит промежутку [-6; 0), так как он больше -6, но меньше 0....

№10. Укажите промежуток, которому принадлежит корень уравнения А) [-12; -6); Б) [-6; 0); В) [0; 6); Г) [6; 12); Д) [12; +∞).