1.58. Докажите, что при любом натуральном п 2^n+2^n=2^n+1 выполняется равенство

Другие вопросы по теме Алгебра
Популярные вопросы
- Что или кто может навредить журавлю-красавке....
3 - Нужно решить второе неравенство методом интервалов!...
2 - Коммерческая организация некоммерческая организация государство нужно соотнести...
3 - Птах 12см и 12м сова сколько всего. решити...
3 - Информация о лохнеском чудовизе на . ! через 30 минут в школу...
1 - 1. какая композиционная и смысловая связь устанавливается в рассказе между...
3 - вопросы. 1)с кем вы познакомились в начале рассказа? прочитайте данный...
1 - 4.1+(-8..+1.9)= и уравнения х-5.16=-2.15 (1.5-х)-2.8=16.2 решите...
2 - Напишите синквейн 1) 1 сущ( тема) 2) 2 прил 3) 3 гл 4) фраза ( отношение...
3 - Решите уравнение : 3*(2х+3)-5*(7-4х)-2*(5х+4)=-2...
3
Смотрите объяснение!
Объяснение:
Так как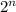 - показательная функция, то
- показательная функция, то 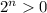 при
при  (по условию)
(по условию)
Прологарифмируем выражение с логарифмом по основанию 2: