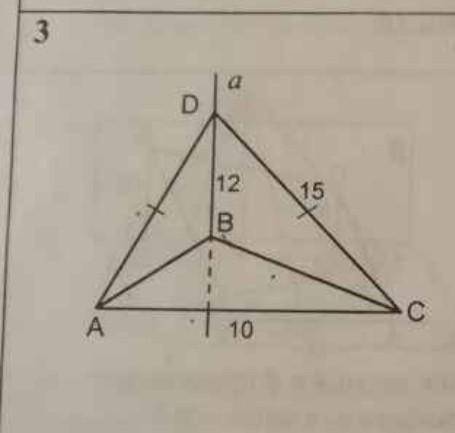
Прямая а перпендикулярна плоскости АВС. Найти расстояние между прямыми а и АС.​

Для решения данной задачи, нам необходимо использовать основные понятия геометрии, такие как плоскости, прямые и углы. Давайте разберемся сначала с понятием перпендикулярных прямых и плоскостей.

Перпендикулярные прямые - это прямые, которые пересекаются и образуют прямой угол (угол величиной 90 градусов).

Перпендикулярные плоскости - это плоскости, которые пересекаются и образуют прямую (или также называемую линию) пересечения.

Теперь, чтобы найти расстояние между прямыми "а" и "АС", мы должны использовать следующий подход:

Шаг 1: Определить точки, через которые проходят данные прямые.
На рисунке даны плоскость ABC, прямая "а" и прямая "АС". Пусть точка D на прямой "а" является точкой пересечения прямой "а" и плоскости ABC, а точка E является произвольной точкой на прямой "АС".

Шаг 2: Провести перпендикуляры из произвольной точки E на прямую "а" и плоскость ABC. Обозначим эти перпендикуляры как EH и EG соответственно.

Шаг 3: Убедиться, что данная постановка вопроса позволяет нам применить теорему Пифагора, которая гласит: "В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин других двух сторон." Или в математической форме: c^2 = a^2 + b^2.

Шаг 4: Заменить стороны прямоугольного треугольника необходимыми данными из постановки задачи.
Строим прямоугольный треугольник DEG с длиной EG (сторона а) и DH (длина АС). Также длина EG является гипотенузой и выражается через DE (длина перпендикуляра на плоскость ABC) и HE (длина перпендикуляра на прямую "а").

Шаг 5: Записываем уравнение нашего прямоугольного треугольника DEG в виде уравнения Пифагора:
EG^2 = DE^2 + HE^2

Шаг 6: Выражаем DE и HE через данные из задачи.
Из постановки вопроса видно, что EG (а) и DH (АС) являются площадными диагоналями и образуют прямой угол. Таким образом, мы можем записать следующие соотношения:
EG = DH^2
DE = DH * tan(угол, который прямая "а" образует с плоскостью ABC)

Шаг 7: Подставляем выражения для EG и DE в уравнение прямоугольного треугольника DEG:
DH^2 = (DH * tan(угол, который прямая "а" образует с плоскостью ABC))^2 + HE^2

Шаг 8: Решаем полученное уравнение относительно DH и находим искомое расстояние между прямой "а" и "АС".

В заключение, для решения данной задачи мы использовали геометрические концепции перпендикулярности прямых и плоскостей, а также теорему Пифагора. Используя эти инструменты, мы смогли получить математический подход к решению задачи и выразить расстояние между прямыми "а" и "АС" с помощью выражения, которое можно вычислить.