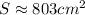Вычислите объем и площадь поверхности шара ,если площадь сечения проходящего через центр шара равен 64 пи см в квадрате. ответ укажите от точности до целых
Другие вопросы по теме Геометрия
Популярные вопросы
- Классификация неорганических и органических веществ. 2 вариант. 1. В перечне веществ,...
3 - «Преобразование тригонометрических выражений»...
2 - Надо обпределить климатическую область умеренного пояса,в котором расположены данные...
3 - Поясніть під дією яких чинників склалася міжнародна спеціалізація острівних країн...
3 - Подобрать к глаголам видовую пару, подчеркнуть чередующиеся согласные, указать...
2 - Запишите число 60 в виде произведения двух цельных положительных множителей. сколько...
2 - Профсоюзная организация АО «Кваза» вышла на администрацию с предложением внести...
1 - Какова мощность тока в каждом из резисторов (см.рис.), если напряжение на источнике...
2 - Опиши космический корабль после полета...
1 - М.Е. Салтыков-Щедрин Премудрый пескарь 1. Литературный жанр произведения Премудрый...
1
Сечение проходящее через центр шара, является осевым сечением, и представляет из себя круг. Тогда площадь сечения будет равна:
Отуда находим радиус сечения
Так как сечение является осевым, радиус шара будет равен радиусу сечения, тогда площадь шара будет равна:
А объем шара будет равен:
ответ: